Unter
https://www.mathelounge.de/683351/folgendarstellung-auf-einem-aufgewickelten-zahlenstrahl
hatte ich die Folge der Potenzen von 2 auf einem Zahlenstrahl dargestellt, der auf einem Kreis mit 101 Punkten aufgewickelt war, und Glied für Glied durch je eine Sehne verbunden. Dabei erhielt ich folgendes Bild, welches eine Herzform einhüllt und daher Kardioide genannt wird:
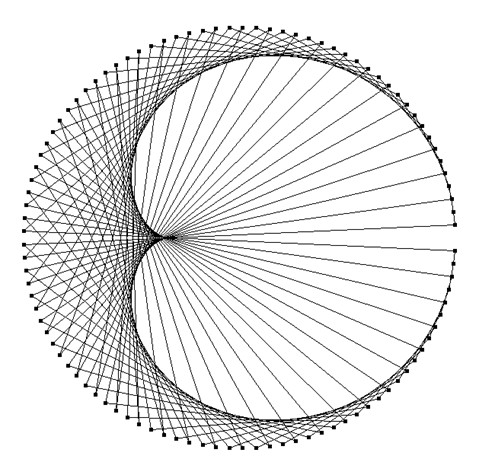
Die Anzahl 101 der Punkte auf dem Kreis war nicht zufällig gewählt. Zahlentheoretisch gesprochen ist die Basis 2 der dargestellten Potenzenfolge eine sogenannte ‚Primitivwurzel‘ von 101. Die Primzahl 101 hat außerdem die Primitivwurzeln 3 7 8 11 12 15 18 26 27 . . . Die Primitivwurzeln zu einer Primzahl findet man unter
https://services.informatik.hs-mannheim.de/KryptoLern/primitive_wurzel.php
Wir wählen nun 3 als Basis der Folgendarstellung und erhalten:
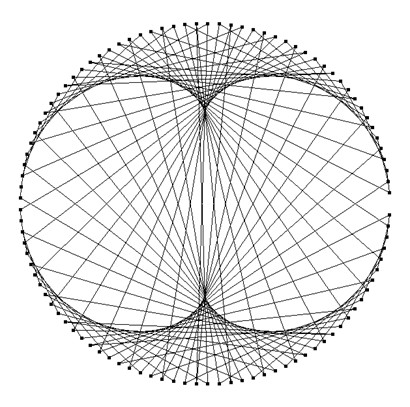
Die eingehüllte Form erinnert an eine Niere und wird daher ‚Nephroide‘ genannt. Nun kennen wir kein Halten mehr und wählen die Primitivwurzel 7 als Basis der Folgendarstellung und erhalten:
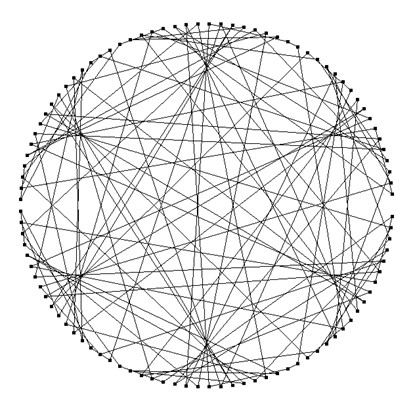
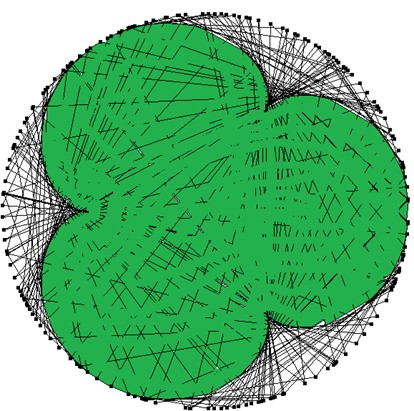
An dieser Stelle kann die Hypothese aufgestellt werden, dass die Anzahl der Einkerbungen der eingehüllten Figur um 1 kleiner ist, als die Basis der dargestellten Potenzenfolge. Der Versuch, auf die gleiche Weise ein vierblättriges Kleeblatt einzuhüllen, hat dieses unbefriedigende Ergebnis:
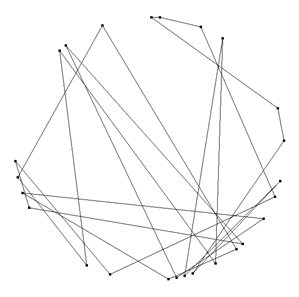
Das liegt, zahlentheoretisch gesehen, daran, dass 5 keine Primitivwurzel von 101 ist. 5 ist allerdings eine Primitivwurzel von 103 und für 103 Punkte auf dem Kreis erhalten wir:
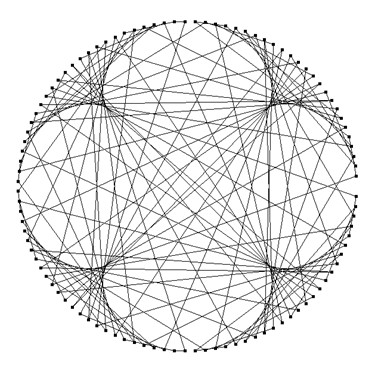
Das Einhüllen eines dreiblättrigen Kleeblattes, könnte man vermuten, gelingt für eine Anzahl n von Punkten auf dem Kreis, sodass 4 Primitivwurzel von n ist. Aber so sehr man auch sucht, man findet diese Zahl nicht. Zahlentheoretisch gesehen liegt das daran, dass Quadratzahlen niemals Primitivwurzeln sind. Wenn man jedoch 101, 103, 107 und schließlich 109 Punkte auf den Kreis legt und die Darstellungen der Potenzenfolge (4n)nЄN in das gleiche Schaubild zeichnet, kann man das dreiblättrige Kleeblatt einhüllen: