Steckbriefaufgaben, Wendetangente

Question

Bestimmen Sie den Funktionsterm f(x) derjenigen ganzrationalen Funktion vierten Grades,  deren Graph bezüglich der y-Achse symmetrisch ist und bei x = 2 die Wendetangente t mit t(x)= -1 1/3x + 2 2/3 hat.

Bei dieser Aufgabe sollte eigentlich 1/48x^4 - 1/2x^2 + 1 2/3 rauskommen, allerdings komme ich auf diese Antwort nicht.

Meine Ansätze:
ax^4+cx^2+e ist die gesuchte Funktion, 4ax^3+2cx ist die erste Ableitung 12ax^2+2c die zweite
f (2) = 0
f''(2)= 0
-

Könnte mir bitte jemand mit dieser Aufgabe helfen? Schreibe in 3 Tagen einen Test und würde gerne wissen, wie man sowas rechnet...

Answer 1

 

eine Funktion 4. Grades hat die allgemeine Form

f(x) = ax⁴ + bx³ + cx² + dx + e

Wenn deren Graph achsensymmetrisch zur y-Achse ist, fallen alle ungradzahligen Exponenten weg, und die allgemeine Form vereinfacht sich zu

f(x) = ax⁴ + bx² + c

Wir brauchen also 3 Gleichungen für die 3 Unbekannten a, b und c.

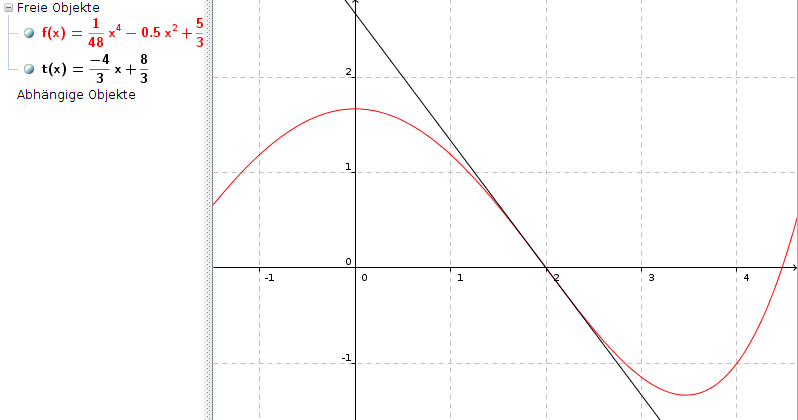
Die Wendetangente

t(x)= -1 1/3x + 2 2/3 = -4/3x + 8/3

hat an der Stelle 2 den Wert

t(2) = -8/3 + 8/3 = 0

die Funktion f(x) natürlich auch, also

f(2) = 0 = 16a + 4b + c

Ferner ist an der Stelle x = 2 ein Wendepunkt, also ist dort die zweite Ableitung = 0:

f'(x) = 4ax³ + 2bx

f''(x) = 12ax² + 2b

f''(2) = 0 = 48a + 2b

Und f(x) hat an der Stelle x = 2 den gleichen Anstieg wie die Wendetangente t(x), also -4/3:

f'(2) = -4/3 = 32a + 4b

Auflösen mit einem vernünftigen Taschenrechner oder per Gauß-Algorithmus ergibt

a = 0,020833333333... = 1875/90000 = 1/48

b = -0,5

c = 1,666666666666... = 15/9 = 5/3

Die gesuchte Funktion lautet also

f(x) = 1/48 * x⁴ - 0,5 * x² + 5/3

 

Besten Gruß

Comments

Sehr gerne :-)

Viel Erfolg beim Test!!

Answer 2

4. Grad, y-Achse symmetrisch und bei \(x = 2\) die Wendetangente \( t(x)=-\frac{4}{3}x + \frac{8}{3}\) 

\( t(2)=-\frac{4}{3}\cdot 2 + \frac{8}{3}=0\)

Symmetrie \(W_1(2|0)\)→ \(W_2(-2|0)\):

\(f(x)=a(x-2)(x+2)(x-N)(x+N)=a(x^2-4)(x^2-N^2)\\=a(x^4-N^2x^2-4x^2+4N^2)\)

\(f'(x)=a(4x^3-2N^2x-8x)\)

\(f''(x)=a(12x^2-2N^2-8)\)

\(W_1(2|...)\):

\(f''(2)=a(48-2N^2-8)=a(40-2N^2)=0\)

\(N^2=20\)

\(m=- \frac{4}{3} \) bei \(W_1(2|...)\):

\(f'(2)=a(32-4N^2-16)=a(16-80)=-64a\)

\(-64a=- \frac{4}{3}\)

\(a=\frac{1}{48}\)

\(f(x)=\frac{1}{48}(x^4-24x^2+80)\)

Comments

eine präzise, zielgerichte Antwort auf die Frage vom 28. Januar 2014:

Schreibe in 3 Tagen einen Test und würde gerne wissen, wie man sowas rechnet...

:)

---

Mir ist klar, dass das mit dem Test nicht hinhaut. Eine zielgerichtete Antwort gab schon "Brucybabe".

Ich habe aber eine weitere Möglichkeit zur Lösung der Aufgabe aufgeschrieben.

---

Es muss nicht immer der Gauß-Algorithmus sein :-)