Aufgabe mit Gerade, Funktion und Schnittwinkel

Question

Aufgabe:

Die Gerade g sei durch den Punkt A(1|-2) und m=1,5 gegeben.

a) Zeichne die Gerade g und berechne ihren Schnittpunkt mit der x-Achse

b)Bestimme den Schnittwinkel von g mit der x-Achse

Problem/Ansatz:

Kann mir da jemand die Aufgabe lösen, also in Schritten. Lösung lautet: P(7/3|0) und m=tan(α) >α=56.3°

Danke!

Answer 1

Hallo

 1.den Punkt einzeichnen sollt dir doch möglich sein m=1,5=3/2 also vom Punkt 2 nach rechts 3 nach oben gibt den 2 ten Punkt, und die 2 verbinden die Gerade.

2.Gleichung y=1,5x+b den Punkt (1,-2) einsetzen gibt b, oder in der Zeichnung den y Abschnitt b ablesen.

3. y=0 setzen, x ausrechnen, (in der Zeichnung kontrollieren

4. arctan(1,5) =α mit TR bestimmen arctan=tan^-1 auf manchen TR

Gruß lul

Answer 2

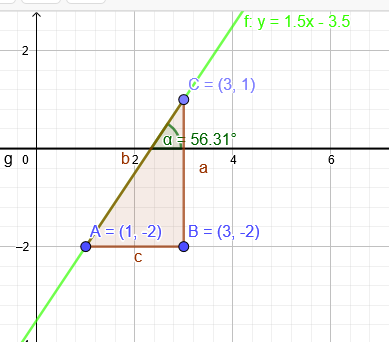
"Die Gerade g sei durch den Punkt A(1|-2) und m=1,5 gegeben."

Punkt-Steigungsform der Geraden:

\( \frac{y-(-2)}{x-1} \)=1,5

\( \frac{y+2}{x-1} \)=1,5

y=1,5x-3,5  

a)Schnittpunkt mit der x-Achse: y=0

1,5x-3,5 =0

x=\( \frac{3,5}{1,5} \)≈2,33

b)Bestimme den Schnittwinkel von g mit der x-Achse

\( tan^{-1} \)(1,5)=56,31°

Comments

Hey, danke. erklärst wahnsinnig gut und mit Grafiken, will nicht frech sein, aber kannst du mir noch bei der neuen gestellten Frage kurz helfen :D

sry und DANKE