Aufgabe:
Die Mittelpunkte A, B, C dreier kongruenter Kreise, die keine gemeinsamen Punkte haben, liegen nicht auf derselben Geraden.
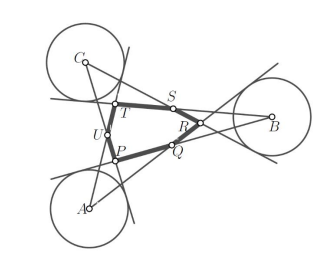
Von den Punkten A, B, C werden die sechs in der Abbildung gezeigten Tangenten an die Kreise gelegt, die ein konvexes Sechseck einschließen.
Es ist zu beweisen, dass die Längen von drei paarweise nicht unmittelbar benachbarten Seiten dieses Sechsecks gleich sind, also dass gilt:
|QR| + |ST| + |UP| = |PQ| + |RS| + |TU|
Problem/Ansatz:
Ich habe daran jetzt schon eine ganze Weile geknobelt, bin aber zu keinem befriedigendem Ergebnis gekommen.
Ich bin mir mittlerweile recht sicher, dass das Ganze irgendwas mit Dreiecken und vielleicht auch noch Winkeln zu tun hat, aber komme nicht mehr weiter.
Hilfe wäre wirklich toll, dankeschön :)