Wie groß ist der Funktionswert f(x) im Punkt B?

Question

Kann mir jemand bei dieser Aufgabe helfen komm nicht ganz drauf was die Werte für B sein sollen, habs mit Geogebra, und einfach die 1 Ableitung davon gemacht und die beiden Funktionen geschnitten, aber das Ergebnis war falsch:-S

Text erkannt:

Die folgende Grafik zeigt drei kritische Punkte der Funktion \( f(x) \) bzw. ihrer Ableitung \( f^{\prime}(x) \). Die Funktion ist gegeben durch:
\( f(x)=1.18 x^{3}-1.39 x^{2}-1.07 x+2.15 \)
Wie groß ist der Funktionswert \( f(x) \) im Punkt B?

Answer 1

B scheint der Wendepunkt zu sein. Du musst also die zweite Ableitung Null setzen und mit dem erhaltenen Wert x den Funktionswert f(x) berechnen.

Answer 2

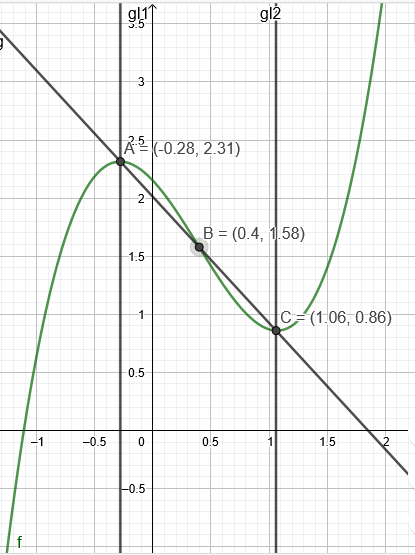
\(f(x)=1,18 x^{3}-1,39 x^{2}-1,07 x+2,15 \)

\(f´(x)=3,54 x^{2}-2,78 x-1,07 \)

Extremwerte:

3,54x^2-2,78x-1,07=0

x₁≈-0,28    y₁ ≈2.31

x₂≈1,06      y₂≈-0.86

Koordinaten von B: x=\( \frac{-0.28+1.06}{2} \)=0,39

y=\( \frac{2,31+0,86}{2} \)=1,58

Das ist nun auch der Wendepunkt von f(x).

Wenn du die 2. Ableitung 0 setzt, bekommst du den x-Wert des Wendepunktes. Der y -Wert ist dann der gesuchte Funktionswert.

Comments

Wäre dann die Antwort: 1,58?

weil unter Funktionswert versteht man die y-werte oder?

VIELEN DANK

Answer 3

f ( x ) = 1.18 x^3 - 1.39 x^2 - 1.07 x + 2.15
f´(x ) = 3.54 x^2 - 2.78 x - 1.07
f ´´ ( x ) = 7.08 * x - 2.78
7.08 * x - 2.78 = 0
x = 0.3927
f ( 0.3927) = 1.587

W ( 0.3927 | 1.587 )

Comments

Ist dann die Antwort also der gesuchte Funktionswert (x) von B = 1,58?

---

Ja, Fülltext. Siehe Graph Moliets.