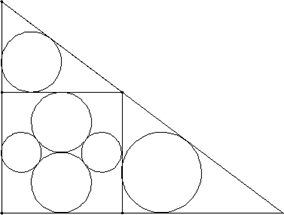
Auf der Mittelparallelen eines Quadrates mit der Seitenlänge 4r liegen zwei gleichgroße sich berührende Kreise mit dem Radius r. Diese haben je eine Quadratseite als Tangente. Sie berühren zwei Kreise mit dem Radius t, von denen je einer eine andere Quadratseite als Tangente hat. Zwei Seiten des Quadrats liegen auf den Katheten eines rechtwinkligen Dreiecks, auf dessen Hypotenuse ein Eckpunkt des Quadrates liegt. Die Flächenstücke, die nach Entnahme des Quadrats vom rechtwinkligen Dreieck übrig bleiben, sind wiederum zwei rechtwinklige Dreiecke, deren Inkreise die Radien r (wie oben) und R haben. Zeige: R=2t (t wie oben).