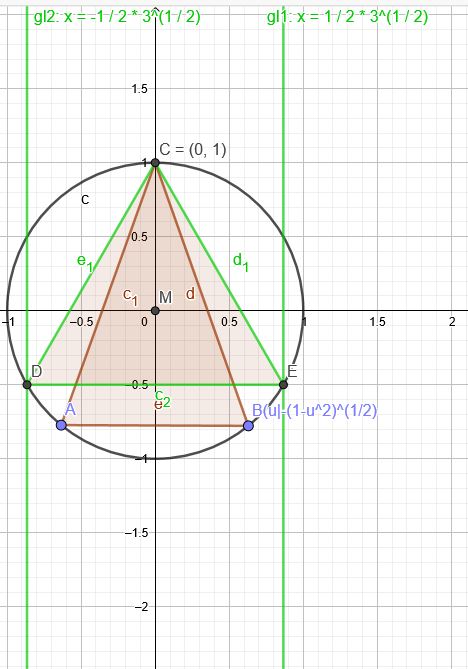
Falls die Optimallösung gesucht werden soll:
Lösungen Teilaufgaben sind schon dabei.
\(A(u)=u*(1+ \sqrt{1-u^2}) \) soll maximal werden.
\(A(u)=u+u* \sqrt{1-u^2}) \)
\(A(u)=u+\sqrt{u^2-u^4} \)
\(A´(u)=1+\frac{2u-4u^3}{2*\sqrt{u^2-u^4}}\)
\(A´(u)=1+\frac{u-2u^3}{\sqrt{u^2-u^4}}\)
\(1+\frac{u-2u^3}{\sqrt{u^2-u^4}}=0\)
\(\sqrt{u^2-u^4}=2u^3-u |^{2}\)
\(u^2-u^4=4u^6-4u^4+u^2\)
\(4u^6-3u^4=0\)
\(u^4*(4u^2-3)=0\)
\(u₁=0\) kommt nicht in Betracht.
\(u^2=\frac{3}{4}\)
\(u₂=\frac{1}{2}\sqrt{3}\)
\(u₃=-\frac{1}{2}\sqrt{3}\)