Anhang: Wieso gibt es zwei verschiedengrosse Kreise die der Ellipse eingeschrieben werden können?

Question

Aufgabe:

Schrägschnitt schräger Kegel kleine Halbachse der Ellipse bestimmen.

Problem/Ansatz:

Anhang: Wieso gibt es zwei verschiedengrosse Kreise die der Ellipse eingeschrieben werden können?

Text erkannt:

AB schuittebeve 1

Text erkannt:

AB schuittebeve 1

Comments

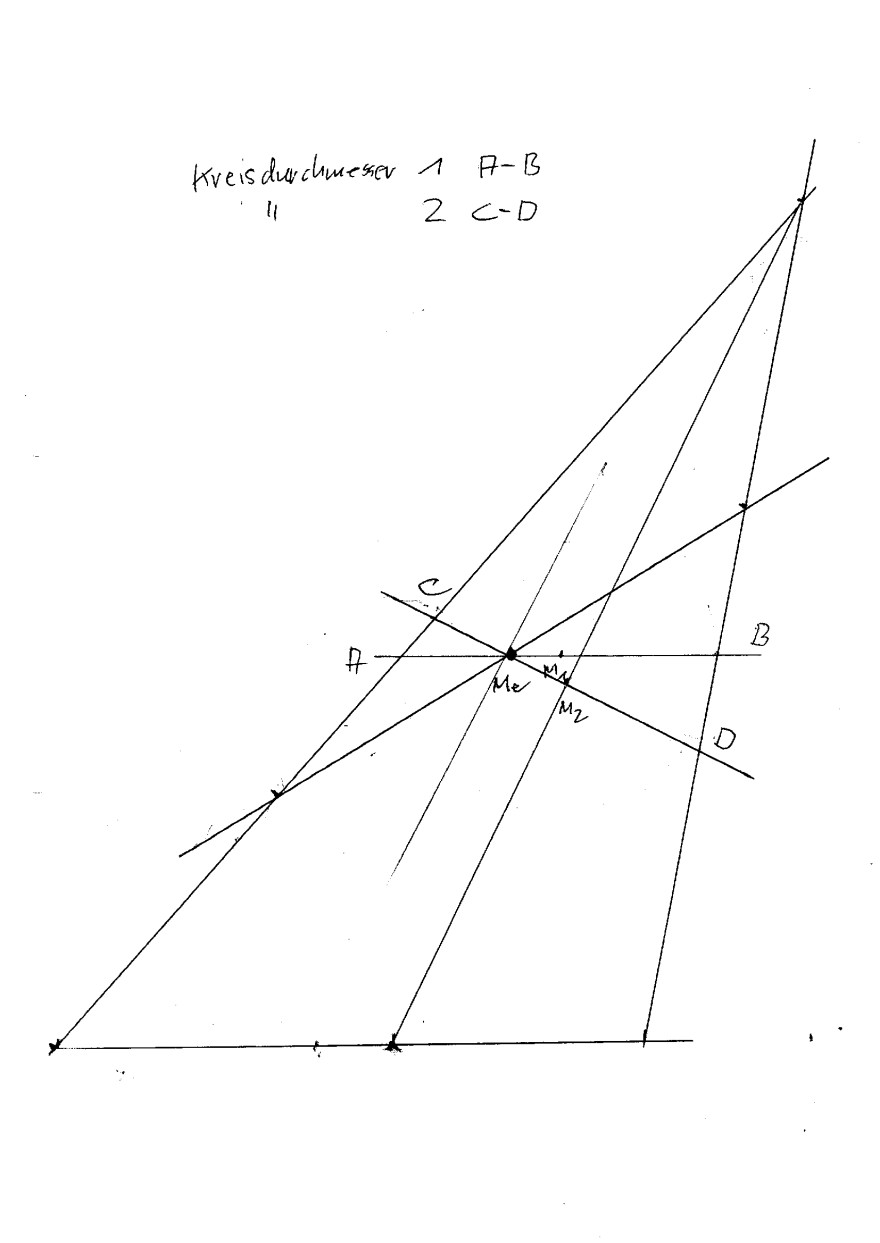
Vom Duplikat:

Titel: Schrägschnitt schräger Kegel, 2 Lösungen möglich?

Stichworte: ellipse,lineare-gleichungssysteme

Aufgabe:

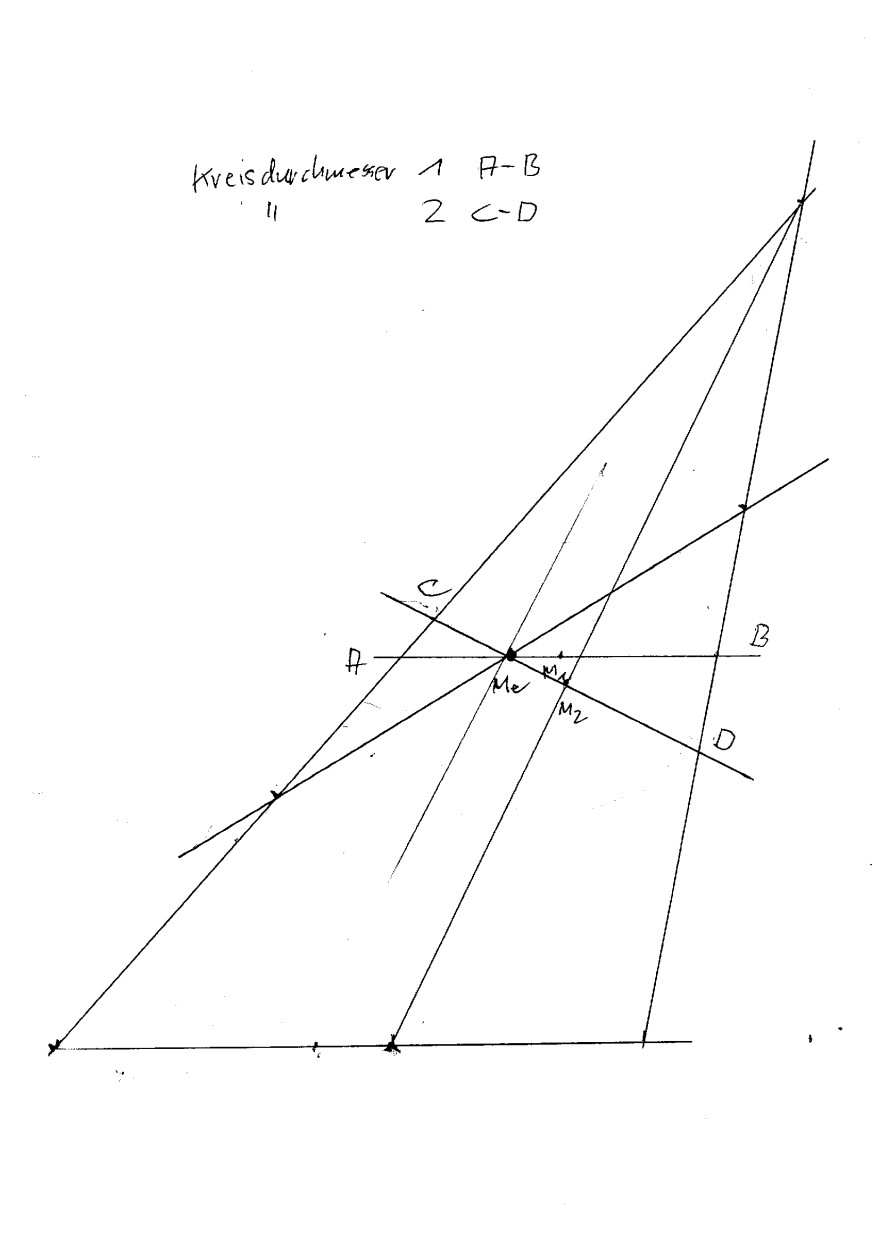
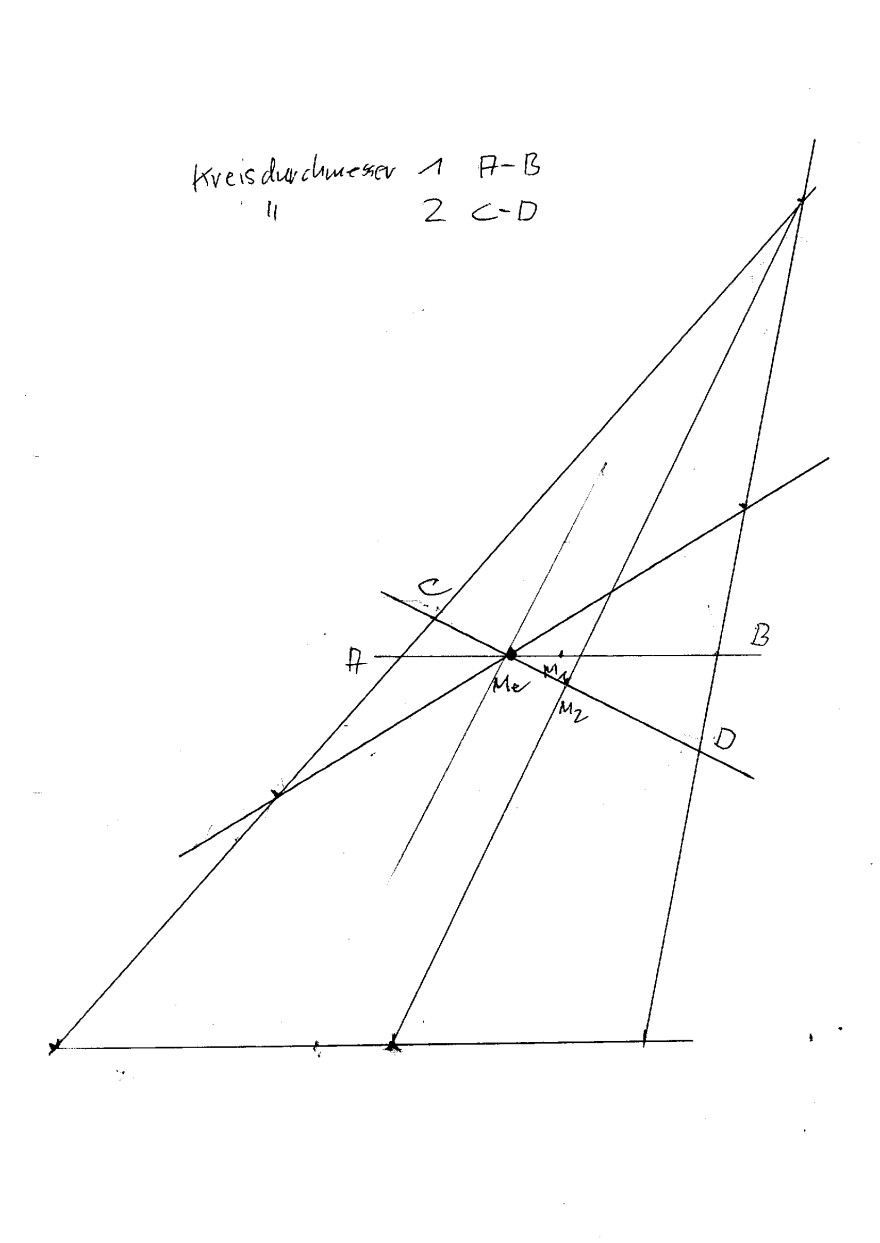
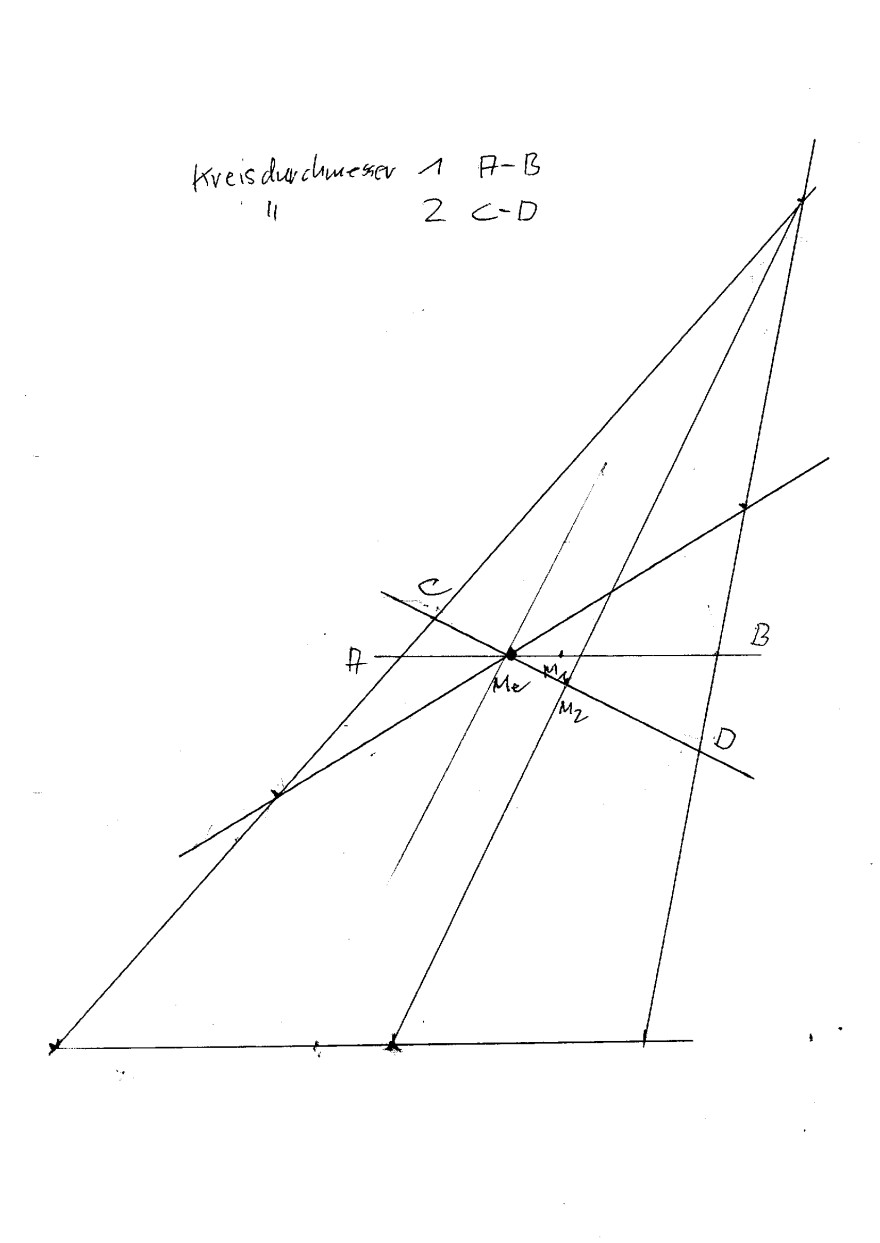
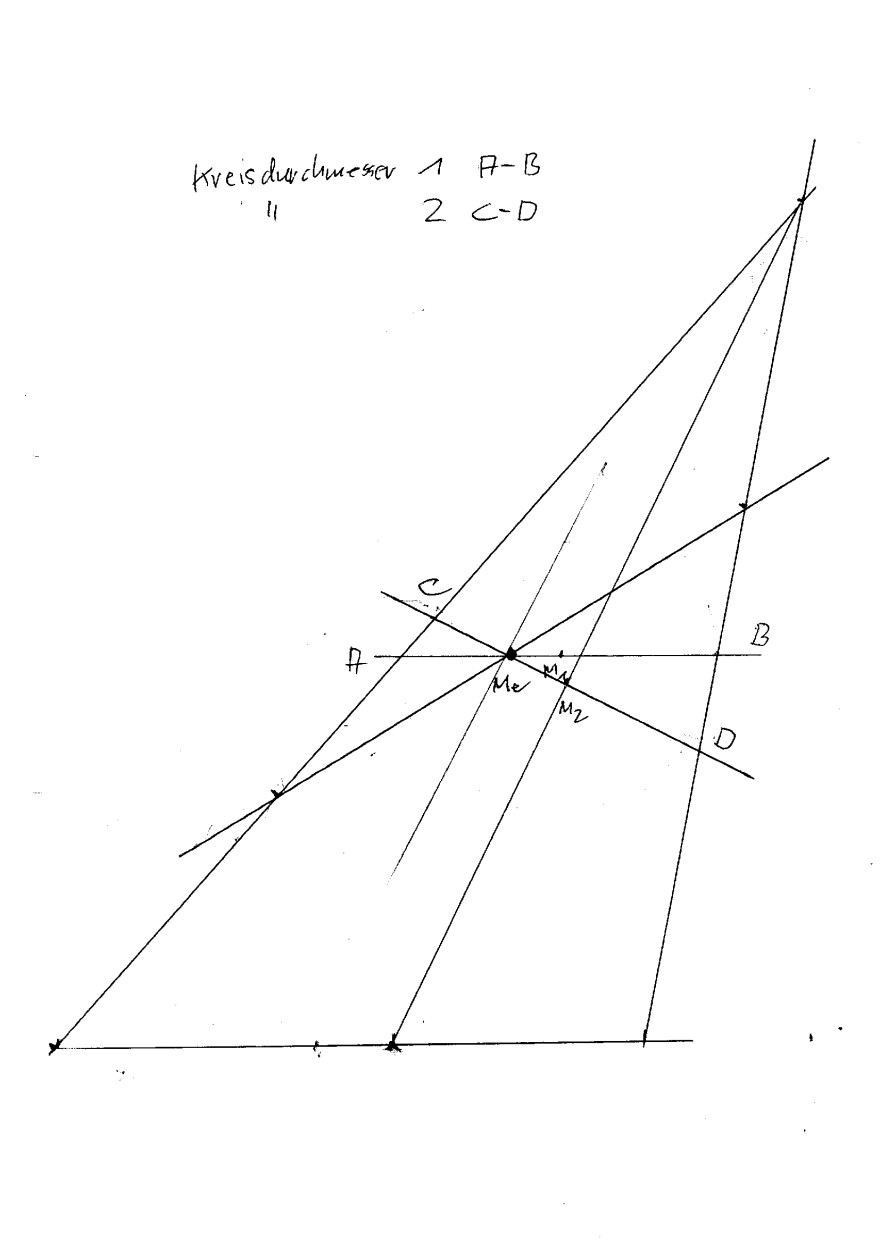
Bei Schrägschnitten eines schrägen Kegels gibt es offenbar mehrere Lösungen für die kurze Halbachse der entstehenden Ellipse.

Problem/Ansatz:

Im Anhang sind die beiden Lösungen eingezeicn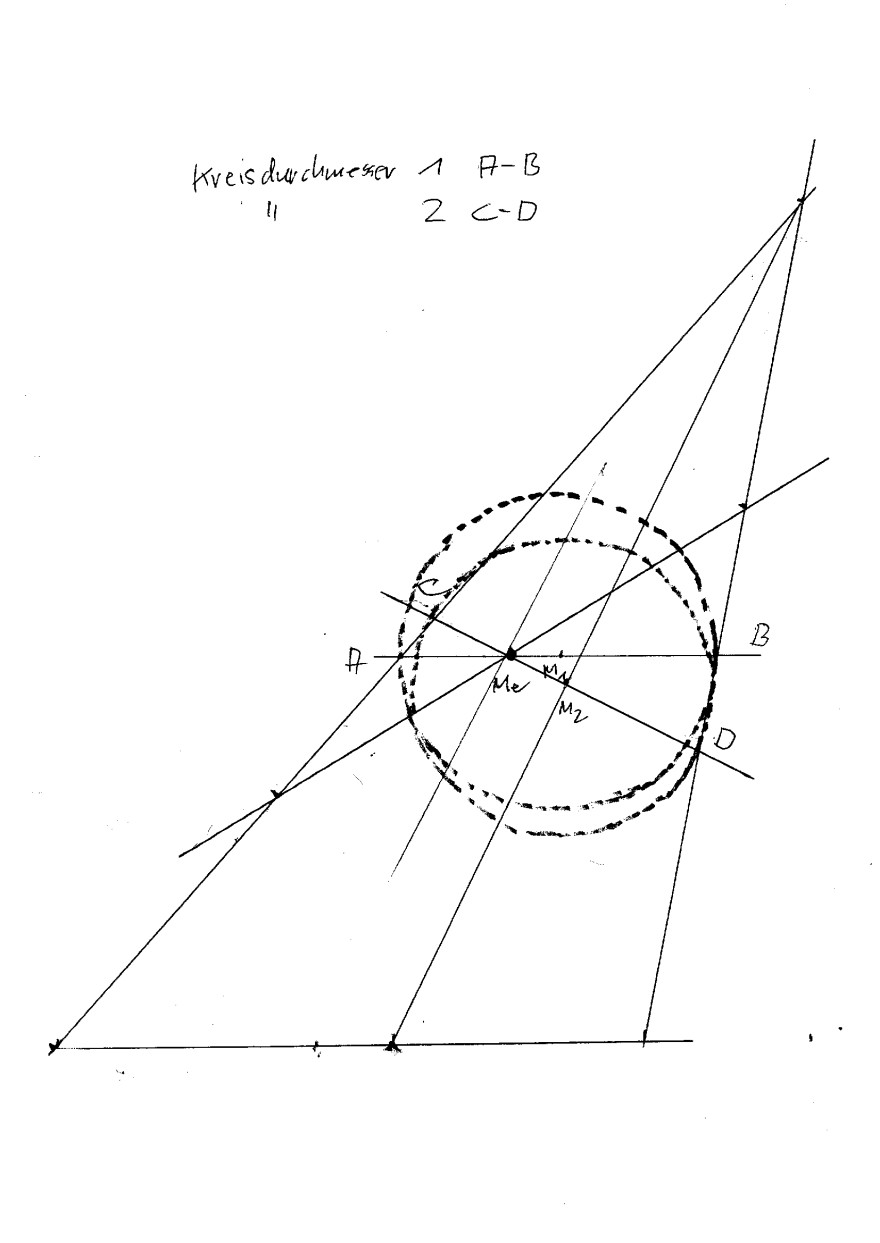 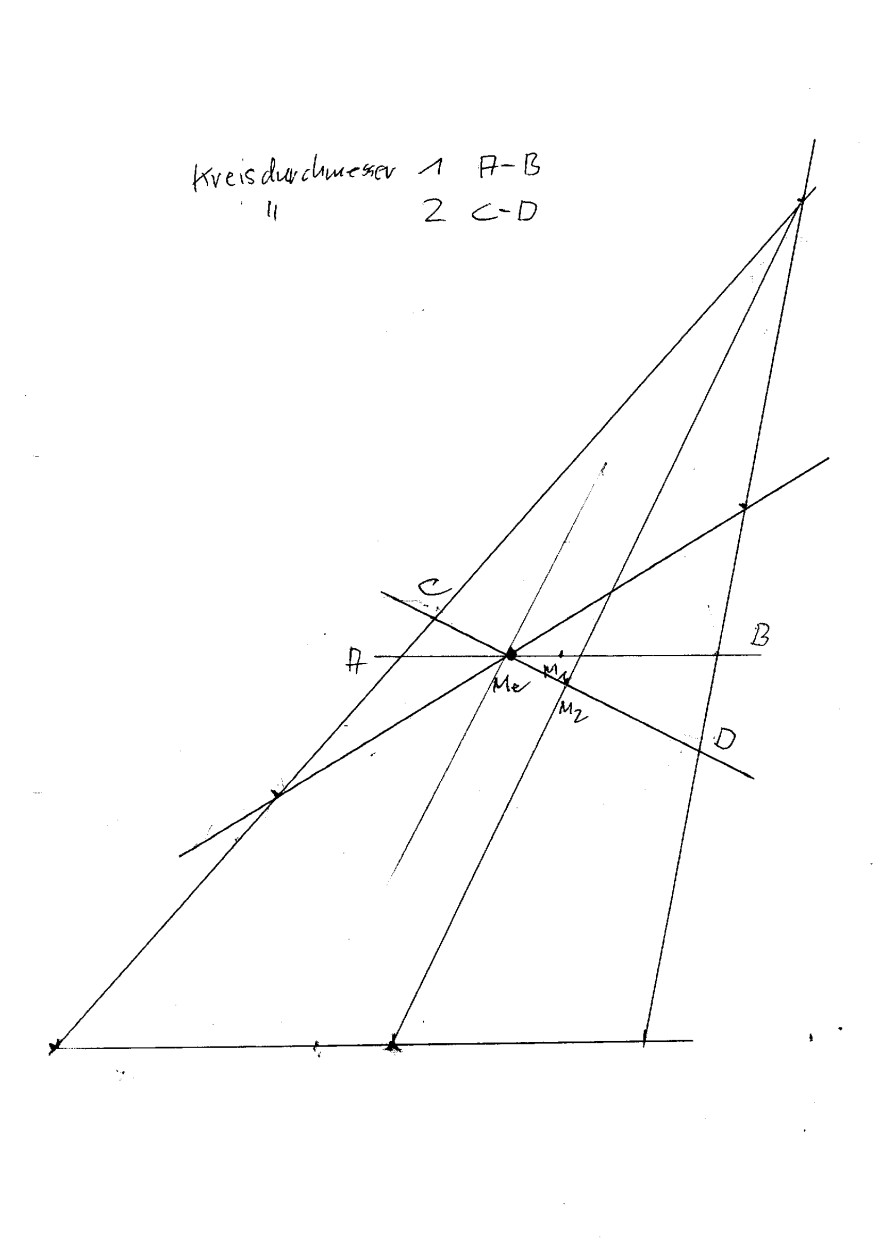het.

Answer 1

Grüezi Charly,

Wieso gibt es zwei verschiedengrosse Kreise die der Ellipse eingeschrieben werden können?

Weil der Kreis mit Durchmesser \(CD\) kein Kreis ist, sondern eine Ellipse.

schau Dir mal die Definition von schiefer Kreiskegel an. Kreise sind nur die Schnitte die parallel zur kreisförmigen Grundfläche liegen.

Gruß Werner

Comments

Lieber Werner

Vielen Dank für die überzeugende Grafik.

Jetzt habe ich es endlich begriffen.

Charly