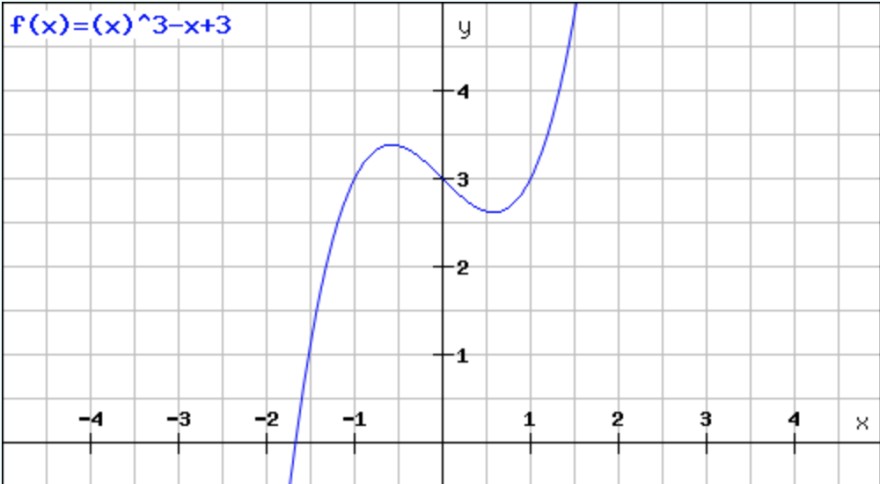
Aufgabe:
Konstruieren Sie ein Beispiel für eine Funktion f : ℝ>0 → ℝ, die strikt konvex, aber nicht monoton ist. (Es reicht einen aussagekräftigen Funktionsgraphen anzugeben).
Problem/Ansatz:
Mein Ansatz wäre folgender:
1) Eine strikt konvexe Funktion liegt vor, wenn die zweite Ableitung > 0 ist.
2) Zusätzlich darf die Funktion nicht monoton sein, d.h. Sie müsste im ersten Quadranten (x>0) monoton fallen und steigen, also eine Potenzfunktion sein?
Ich habe versucht etwas rumzuprobieren und wäre nun bei folgender Funktion angelangt, dessen zweite Ableitung f''(x) = 6x ist und somit für alle x > 0 strikt konvex sein müsste. Ist dies korrekt?