2 mathematische Darstellungsformen für die Errorfunktion

Question

Graph der Errorfunktion / Gaußsches Fehlerintegral

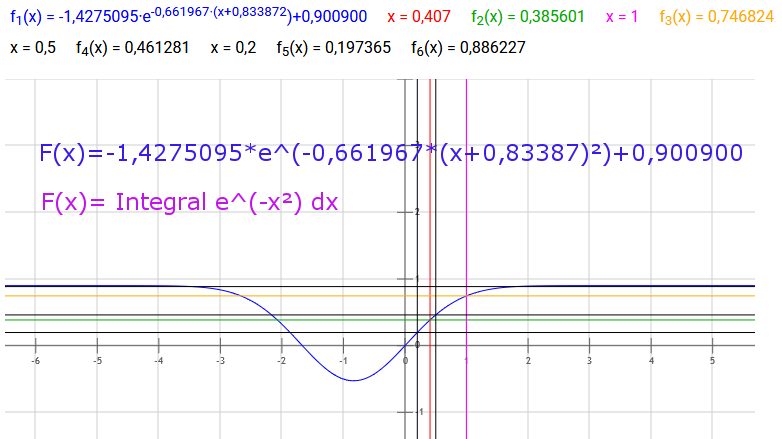
Die im Bild eingezeichneten 4 Wertepaare (= 4 Konstanten, iterativ) wurden von einem Online-Rechner für die Fehlerfunktion übernommen, ....auch so lässt sich die Errorfunktion berechnen!

F(x)=-a*e^(-b*(c+x)^2)+d

Berechnung des Integrales von y=e^(-x^2)dx=(pi)^0.5*erf(x)/2, Gaußsches Fehlerintegral

innere Funktion: u=-x^2 Integral u(x)dx=-1/3*x^3

äußere Funktion: Ableitung e^u=e^u

Produkt dieser beiden Terme mit dem konstanten Faktor a: -1/3x^3*e^(-x^2)*a=Integral e^(-x^2)dx

Ableitung bilden: (-x^2*e^(-x^2)+2/3*x^4*e^(-x^2))*a=e^(-x^2), daraus folgt:

a=1/(-x^2+2/3x^4)

damit ergibt sich das Integral e^(-x^2)dx=pi^0.5*erf(x)/2=-1/3*x^3*e^(-x^2)*a !!!!!!!!!!!

Damit wurde meine Rechentechnik, in Bezug auf das Berechnen der Integrale von Innen nach Außen bestätigt, .....wie bei einer Funktionsaufschlüsselung!

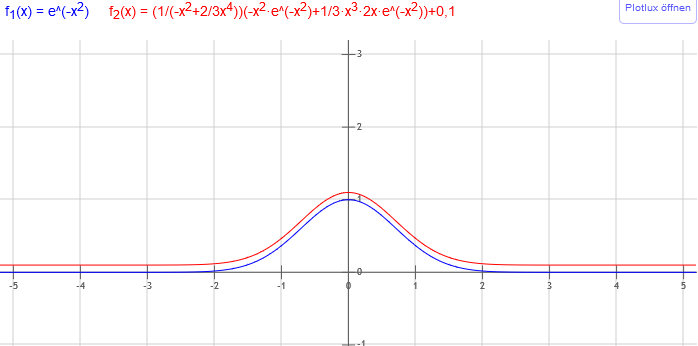
Probe der Ableitungen:

f'₁(x) = e^(-x^2)    f'₂(x) = (1/(-x^2+2/3x^4))*(-x^2*e^(-x^2)+1/3*x^3*2x*e^(-x^2))=e^(-x^2)

es wurde auch ein spezieller Wert der Stammfunktionen berechnet/überprüft, mit identischen Ergebnissen

meine Frage: Ist dies alles korrekt?

Danke für die Antworten! Bert Wichmann!

Muß dazusagen, daß ich diese Aufgaben schon einmal eingestellt hatte, habe damals jedoch etwas übersehen....!

Möchte auch sichergehen, daß dies alles so stimmt!

Answer 1

Wodrin liegt der Vorteil eine einfache Funktion durch eine komplizierte anzunähern?

Außerdem, wähle \( a=-1 \ ; c=0 \ ; b =1 \ ; d=0 \) dann folgt

$$ F(x) =e^{-x^2} $$ Ist doch viel einfacher!

Comments

F(x) ist aber die Stammfunktion/das Integral von e^(-x^2).....

übersetzt heisst dies: habe den Graphen e^(-x^2) an der x-Achse gespiegelt und dann durch iteratives Rechnen die einzelnen Faktoren ermittelt, so daß die Stammfunktion/das Integral von e^(-x^2) das Resultat war.....

Answer 2

Hallo

Dein Fehler

-1/3x3*e^(-x2)*a=Integral e^(-x2)dx du schreibst nur a nicht a(x) später hast du aber sehr wohl a(x)

also musst du in Wirklichkeit -1/3x3*e^(-x2)*a(x)=Integral e^(-x2)dx differenzieren mit der Produktregel, dadurch hast du am Ende nicht a(x) wie du rechnest, sondern eine Differentialgleichung für a(x)

daran führen auch viele !!!! Zeichen nicht vorbei.

wo soll dein Integral denn anfangen? vielleicht läßt du dir mal erf(x) platten, vielleicht von wolfram, um deinen Irrtum zu sehen.

bis dann, lul

Comments

das mit dem a(x), ein Formfehler, kein Rechenfehler, nehme ich auf meine "Kappe"

die Ableitung ist jedoch korrekt....., vom Rechner ausgeführt worden

---

Ich habe, ehrlich gesagt, nicht nicht verstanden, welche Aussage oder Formel wir überprüfen sollen. Was ist Deine Behauptung?

---

die Ableitung ist jedoch korrekt....., vom Rechner ausgeführt worden. Sie ist nur korrekt, wenn a eine Konstante ist, aber du schreibst dann ja selbst ein a(x)

schreibe  deinen Ausdruck für a(x) an die Stelle von a und lass das wieder vom Rechner ausführen.!

lula

---

Ihr sollt bitte überprüfen ob die beiden aufgezeigten Darstellungsformen für:

F(x)=∫e^{(-x^2)}dx, richtig sind.....!

---

Dazu wollte ich von Dir einmal eine explizite Darstellung der Formel (beide Seiten) lesbar haben - die sehe ich nicht.

---

Hallo

nochmal, es ist nicht korrekt, glaubst du wenigstens dem plot der 2 Funktionen ?

---

.....habe bei dem letzten eingestellten Bild von mir die Ableitung mit dem Rechner ermittelt.... und da stimmte alles, habe dies nicht per Hand überprüft....., "blindes Vertrauen....."

wenn a als Konstant anzusehen ist, auch wenn es ein a(x) ist, stimmt die Berechnung, aber es ist nun mal ein a(x)....., Produktregel bei der Differentiation......und da hast Du nun wiederum Recht.....