Hallo,
Vielleicht könne man auch die Länge der Strecke AB berechnen
das ist gar nicht nötig! Machen wir es mal gaaaanz ausführlich.
Einen (beliebigen) Punkt auf der Strecke \(AB\) kann man darstellen durch$$T(\lambda) = (1-\lambda)A + \lambda B, \quad 0\le \lambda \le 1$$Das entspricht der Formulierung \(T(\lambda)=A + \lambda(B-A)\), die Dir vielleicht eher geläufig ist
Jetzt lautet die Forderung$$\frac{|AT|}{|TB|} = \frac{2}{1} $$Um eine Distanz zwischen zwei Punkten zu bestimmen, benötigt man zunächst mal den Vektor von einem Punkt zum anderen. Also gilt es \(T-A\) und \(B-T\) zu berechnen:$$\vec{AT}=T-A = -\lambda A + \lambda B = \lambda(B-A) \\ \vec{TB} = B -T = (1-\lambda)B -(1-\lambda)A = (1-\lambda)(B-A)$$und das setze man einfach in Forderung (s.o.) ein:$$\begin{aligned} \frac{|AT|}{|TB|}&= \frac{| \lambda(B-A)|}{|(1-\lambda)(B-A)|}\\ &= \frac{\lambda\cdot| B-A|}{(1-\lambda)\cdot|B-A|} \\ &= \frac{\lambda}{1-\lambda}\\ &= 2&&|\,\text{lt. Forderung s.o.}\\ \implies \lambda &= 2-2\lambda\\ 3\lambda &= 2\\ \lambda &= \frac23 \end{aligned}$$Womit das \(\lambda\) berechnet wurde, für das die Forderung erfüllt ist, unabhängig von den Werten von \(A\) und \(B\). Für den konkreten Wert \(T\) bleibt bloß das Einsetzen der Koordinaten von \(A\) und \(B\)$$T = \left(1-\frac23\right)\begin{pmatrix}1\\ 0\\ -1\end{pmatrix} + \frac23 \begin{pmatrix}4\\ 6\\ 5\end{pmatrix} \\\phantom{T}= \frac13\begin{pmatrix}9\\ 12\\ 9\end{pmatrix} = \begin{pmatrix}3\\ 4\\ 3\end{pmatrix}$$
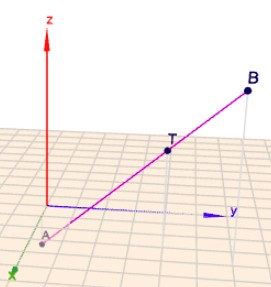
Gruß Werner
PS.: wenn man aber weiß, dass es von 1 bis 4 drei Schritte sind und dass man nach dem zweiten Schritt (bei der 3) von 1 doppelt so weit entfernt ist, wie von der 4, dann hätte man dieses Ergebnis auch gleich hinschreiben können.
PPS.: übrigens hat jeder Punkt \(T'\) im Raum, der auf der Kugeloberfläche einer Kugel mit dem Radius \(6\) und Mittelpunkt bei \((5|\,8|\,7)\) liegt, die Eigenschaft$$|AT'| \div |T'B| = 2\div 1$$so zum Beispiel \(Q(7|\,4|\,3)\) da \(|AQ| = 2\sqrt{17}\) und \(|QB|=\sqrt{17}\). Aber nur \(T\) (s.o.) liegt auch auf der Strecke \(AB\)