erst einmal meine Skizze für f2(t) - ich hoffe, sie stimmt mit Deiner überein:
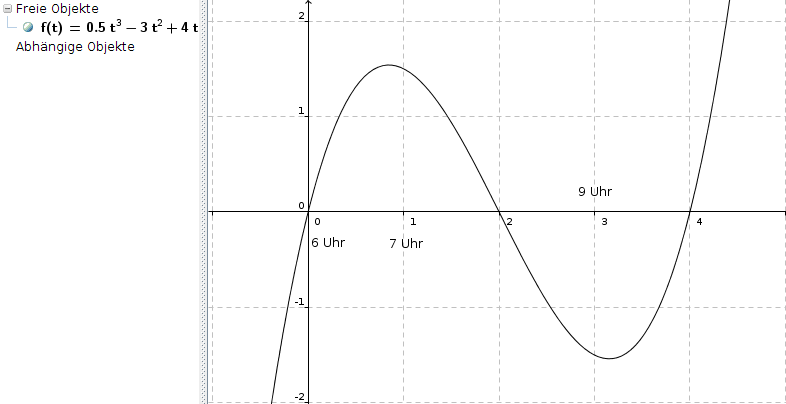
f(t) = 0,5t3 - 3t2 + 4t
Bedeutung positiver und negativer Funktionswerte dieser Funktion:
f(t) beschreibt die Änderungsrate der Staulänge; deshalb bedeutet jeder positive Funktionswert eine Zunahme dieser Länge, jeder negative Wert eine Abnahme.
Achtung: Auch zwischen 7 Uhr und 8 Uhr nimmt die Staulänge zu, wenn auch nicht so stark wie zuvor. Erst ab 8 Uhr nimmt die Staulänge ab, weil dann f(t) < 0.
Wann nimmt die Staulänge am schnellsten zu? Am Maximum von f(t), also
f'(t) = 1,5t2 - 6t + 4 = 0
t2 - 4t + 4/1,5 = 0
t1,2 = 2 ± √(4 - 4/1,5) ≈ 2 ± 1,15
t1 ≈ 3,15
t2 ≈ 0,85
f''(t) = 3t - 6
f''(3,15) = 9,45 - 6 = 3,45 > 0 => Minimum an der Stelle t = 3,15
f''(0,85) = 2,55 - 6 = - 3,45 < 0 => Maximum an der Stelle t = 0,85
Also nimmt die Staulänge am schnellsten um 6 Uhr + 0,85 Stunden zu.
Wann hat der Stau die maximale Länge erreicht?
In dem Moment unmittelbar bevor seine Länge wieder abnimmt; aus der Skizze sieht man, dass dies um 8 Uhr sein muss.
Das gilt, wenn f(t) = 0 ist.
f(t) = 0,5t3 - 3t2 + 4t = t * (0,5t2 - 3t + 4)
t1 = 0 | Da fängt der Stau aber erst an
0,5t2 - 3t + 4 = 0
t2 - 6t + 8 = 0
t1,2 = 3 ± √(9 - 8) = 3 ± 1
t1 = 4
t2 = 2
Im betrachteten Zeitintervall hat der Stau um 8 Uhr seine maximale Länge erreicht.
Hier kann man ganz hübsch den Zusammenhang zwischen f(t) = Veränderung der Staulänge und F(t) = Staulänge sehen:
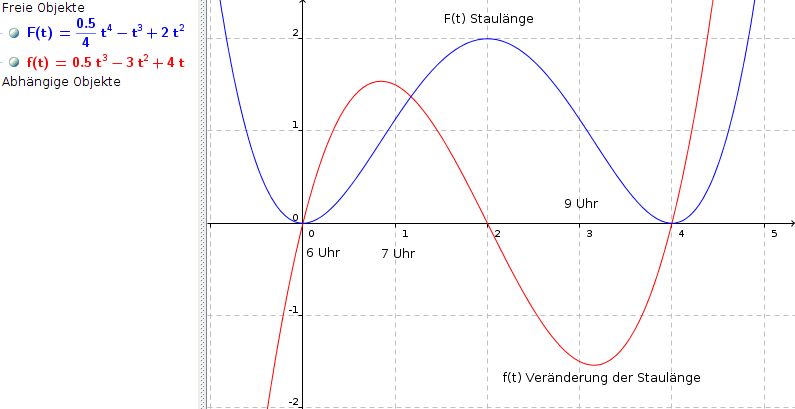
In der Skizze sieht man, dass die maximale Staulänge um 8 Uhr 2km beträgt. Aber wie berechnet man dies?
Wir müssen die Nullstelle von F'(t) finden (notwendige Bedingung für Maximum) und sehen, ob F''(t) an dieser Stelle < 0 ist (hinreichende Bedingung).
Da F'(t) = f(t) ist, wissen wir von oben schon, dass f(2) = 0 ist.
F''(2) = f'(2) = 1,5 * 22 - 6 * 2 + 4 = -2 < 0, also hat F(t) an t = 2 (entspricht 8 Uhr) ein Maximum.
Maximale Staulänge:
F(2) = 0,5/4 * 24 - 23 + 2 * 22 = 2
Term für die Staulänge zum Zeitpunkt t in Abhängigkeit von a:
fa(t) = 0,5t3 - 1,5a * t2 + a2 * t
Staulänge also:
Fa(t) = 0,5/4 * t4 - 0,5a * t3 + a2/2 * t2
Für welche Werte von a beträgt um 8 Uhr die Staulänge 3km?
Fa(2) = 0,5/4 * 24 - 0,5a * 23 + a2/2 * 22 = 3
Die Auflösung nach a machst Du bitte selbst :-)
Besten Gruß