Differenzierbarkeit f'(x) zeigen

Question

Aufgabe:

Sei f: ℝ → ℝ. Zeigen Sie: Ist f differenzierter in x ∈ ℝ, dann gilt  \( \lim\limits_{h\to0} \) \( \frac{f(a+h)-f(a-h)}{2h} \) = f'(x)

Der Beweis ist folgender:

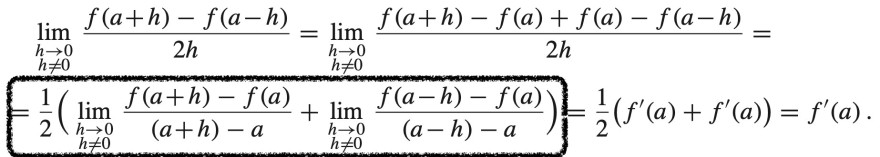
Leider ist für mich nicht klar, wie man auf die Aufteilung von Schritt 2 zu Schritt 3 (umrandet) kommt. Kann mir dies jemand erläutern? Vielen Dank!

Answer 1

Aloha :)

$$\phantom{=}\frac{f(a+h)-f(a)+f(a)-f(a-h)}{2h}$$$$=\frac{\left(\;f(a+h)-f(a)\;\right)-\left(\;f(a-h)-f(a)\;\right)}{2h}$$$$=\frac{f(a+h)-f(a)}{2h}-\frac{f(a-h)-f(a)}{2h}$$$$=\frac12\left(\frac{f(a+h)-f(a)}{h}-\frac{f(a-h)-f(a)}{h}\right)$$$$=\frac12\left(\frac{f(a+h)-f(a)}{h}+\frac{f(a-h)-f(a)}{-h}\right)$$$$=\frac12\left(\frac{f(a+h)-f(a)}{(a+h)-a}+\frac{f(a-h)-f(a)}{(a-h)-a}\right)$$