Nach unten geöffnete Parabel p2 verläuft durch die Punkte P(-1/-5). Berechne die Funktionsgleichung in Normalform.

Question

6. Die Normalparabel p1 hat die Funktionsgleichung y=x²-7x+11

a. Berechnen Sie die Koordinaten des Scheitelpunkts S1 der Parabel p1.

b. eine weitere nach unten geöffnete Parabel p2 verläuft durch die Punkte P(-1/-5)

Ermitteln sie die Funktionsgleichung in Normalform.

c. Berechnen sie die Koordinaten des Scheitelpunkts S2. (Rechnen sie mit p2: y=-x²+5x)

Zeichnen sie beide Parabeln in ein Koordiantensystem.

Comments

Bei b. hast du zu wenige Punkte angegeben.

Answer 1

  1.) habt ihr schon Differntialrechnung ?
       y=x²-7x+11
      y´= 2*x - 7
      2*x - 7 = 0
      2 * x = 7
      x = 3.5
      f (3.5) = 3.5^2 - 7*3.5 + 11
      f ( 3.5 ) = -1.25

     S ( 3.5  l  -1.25 )

  2.) könnte ich aus den Angaben nicht herleiten. Hier fehlt
die Angabe des 2. oder 3.Punktes.

  3.) y=-x²+5x
      S ( 2.5 l 6.25 )

  Zeichnen sie beide Parabeln in ein Koordiantensystem.
  Oben rechts auf dieser Seite ist ein Funktionsplotter.
  Dort kannst du die Funktionen zur Kontrolle rasch zeichnen.

  Bei Fehlern oder Fragen wieder melden.

  mfg Georg
 

Comments

Wollte noch mal fragen wie du auf das 3.) Ergebnis gekommen bist ? :)

 

lg sandy 

---

  die Lösung mit Differntialrechnung

  y=-x²+5x

  y ´ = -2*x + 5
  -2*x + 5 = 0
  x = 2.5
  f ( 2.5 ) = - ( 2.5^2) + 5 * 2.5
  f ( 2.5 ) =  6.25

  S ( 2.5  l 6.25 )

  mfg Georg

Answer 2

c unter der Annahme, dass du noch nicht ableiten kannst.

c. Berechnen sie die Koordinaten des Scheitelpunkts S2. (Rechnen sie mit p2: y=-x²+5x)

y = -x^2 + 5x       |in Scheitelpunktform bringen.

y = - (x^2 -5x)             |quadratisch ergänzen

y = -(x^2 - 5x + 2.5^2 - 2.5^2) 

= -((x^2 - 5x + 2.5^2 ) - 2.5^2) 

= -((x-2.5)^2 - 6.25)

= -(x-2.5)^2 + 6.25

Scheitelpunkt ablesen: S(2.5 | 6.25)

Answer 3

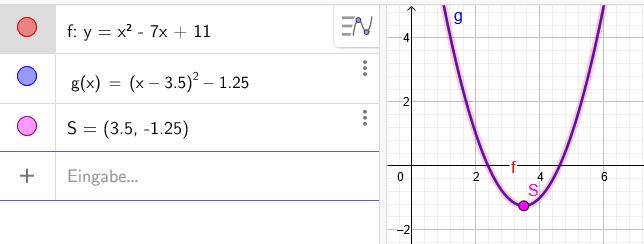
6. Die Normalparabel p1 hat die Funktionsgleichung

 \(y=x^2-7x+11  \)      Umrechnung in die Scheitelpunktform:

\(y=x^2-7x+1  |-11  \)

\(y-11=x^2-7x\)       quadratische Ergänzung:

\(y-11+(\frac{7}{2})^2=x^2-7x+(\frac{7}{2})^2\)        2. Binom:

\(y-11+(\frac{7}{2})^2=(x-\frac{7}{2})^2|+11-12,25\)     Scheitelpunktform:

\(y=(x-3,5)^2-1,25\)

Der Scheitelpunkt hat somit die Koordinaten S\((3,5|-1,25)\)