Ist die Länge etwa 100 Meter oder 230 Meter wie im Buch?

Question

Aufgabe:

HAllo,

es geht um no 10 :

Ist die Länge etwa 100 Meter oder 230 Meter wie Im Buch?

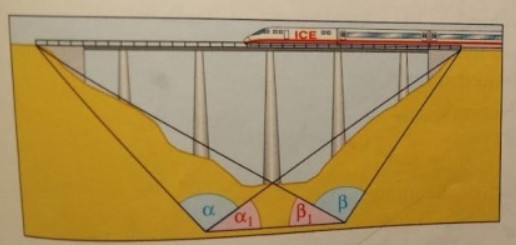
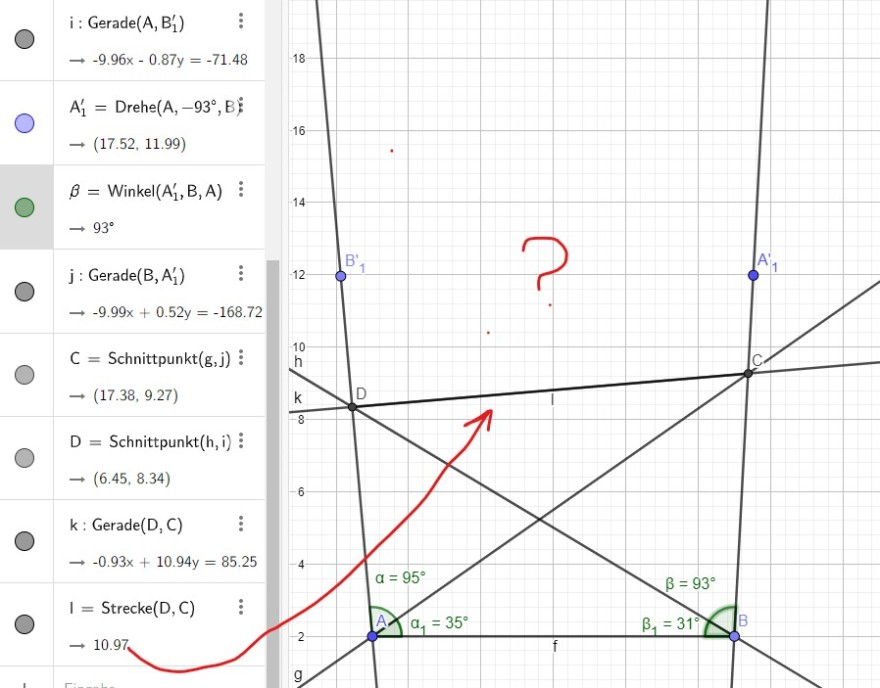
Michel und Nele wollen die Länge einer Eisenbahnbrücke auf folgende Weise ermitteln: Von zwei 100 m voneinander entfernten Stellen einer Straße peilen sie den Anfangs- und Endpunkt der Brücke an und messen Winkel: \( \alpha=95°, \alpha_{1}=35°, \beta_{1}=31° , \beta=93° \) Ermitte mithilfe dieser Werte die Länge der Brücke aus einer maßstabsgetreuen Zeichnung.

Druckfehler in der 1. Auflage: \( \alpha=95^{\circ} ; \alpha_{1}=35^{\circ} ; \beta_{1}=31^{\circ}: \beta=93° \)

Die Brücke ist ungefähr \( 230 \mathrm{~m} \) lang (genauer \( 232 \mathrm{~m} \) ).

Meine Lösung etwa 100 Meter

Comments

Die Winkel Alpha und Beta sind falsch abgetragen. Vermutlich sind das nicht die einzigen Fehler in der Konstruktion.

---

Was meinst du?

Im Buch steht Alpha 95 und Beta 93, oder?

---

und wenn zwischen den messpunkten A und B 100m liegen sollen, dann würde ich das in ggb auch so angeben, etwa A=(0,0), B=(100,0)

---

Du könntest mal mitteilen, was das für ein Buch ist (ISBN oder Autor/Titel/Verlag/Jahr, sowie Seitenzahl der Aufgabe und des Hinweises "205"), damit jemand den Verlag auf den Druckfehler aufmerksam machen kann.

Answer 1

So, hier mal mein Versuch mit GeoGebra:

Das Koordinatensystem wird nicht benötigt, also habe ich es abgeschaltet. Die Hilfspunkte habe ich stehen lassen. Als Maßstab habe ich 1:10 gewählt. (Das ist bei GeoGebra natürlich nicht nötig, aber so kann man es auch mit Papier (A3) und Bleistift machen.) Im Ergebnis bekomme ich eine Brückenlänge von 291,41 m. Vielleicht kann das mal jemand prüfen.

Comments

Ihr scheint alle drei nur einen Teil meines obigen Kommentars berücksichtigt zu haben.

---

Ich räume gerne ein, dass es mir hauptsächlich darum ging, ein wenig mit GeoGebra herumzuspielen. Allerdings finde ich den ggf. in den Buchangaben enthaltenen Fehler nicht, was natürlich nicht heißt, dass es keinen gibt.

---

Im Aufgabentext fehlt die entscheidende Information, dass die Eisenbahnschienen und die Straße in einer Ebene liegen, die ihr aber ohne kritsche Reflektion als selbstverständlich angenommen habt.

---

@hj2166: Warum lieferst du diesen wichtigen und richtigen Kommentar nicht gleich zu Beginn, sondern lieferst zunächst einen für mich kryptischen Kommentar als Einstieg in die Klärung?

---

Vielleicht kann das mal jemand prüfen.

Habe nachgerechnet (nicht gezeichnet). Der Wert stimmt.

Das Buch mit der falschen Musterlösung sollte auf saugfähigem Papier gedruckt werden.

---

Im Aufgabentext fehlt die entscheidende Information, dass die Eisenbahnschienen und die Straße in einer Ebene liegen,...

Stimmt, ohne diese Information wirkt die Aufgabe unterbestimmt.

...die ihr aber ohne kritsche Reflektion als selbstverständlich angenommen habt.

Ja, so ist es gewesen.

---

Hallo,

eine Frage:

Woher fängt Alph=95 und Betta=93? Bedeutet dass Alpha 95 kommt nach Alpha 1? Also ich zeichne zuerst Alpha1= 35 dann nach addiere dazu Alpha=95? Aber dann Alpha wird 35+95 =130 , oder?Ich meine woher kann ich wissen wo fängt Alpha an?

Wie Bild 1

BIld 1

Oder wie BIld 2

Text erkannt:

So, hier mal mein Versuch mit GeoGebra:
Beste?

---

Wo welcher Winkel "anfängt", sieht man auf der Originalzeichnung. Sie sind dort sogar mit unterschiedlichen Farben angemalt.

---

Ja hast du recht , döschwo. ( unterschiedliche Farbe). Jetzt klar

Answer 2

Im Aufgabentext steht, dass die Brücke etwa 230 m lang sei und die Messpunkte auf der Straße 100 m voneinander entfernt.

Comments

Auf dieses Buch kann man sich offenbar überhaupt nicht verlassen.

---

also stimmt meine Lösung döschwo?

---

Gast az0815 hat Dir ja geschrieben, dass die Winkel Alpha und Beta falsch abgetragen sind.

---

Da scheint der Wurm drin zu sein im Buch, ich komme auf eine erheblich längere Brückenlänge als 232 m. Nachgerechnet, nicht nachgezeichnet wie in der Aufgabe gefordert, bekomme ich (unter der Annahme A, B, C und D in einer Ebene):

Ursprung des Koordinatensystems bei A

Winkelsummensatz:

γ = 21°, δ = 19°

Sinussatz:

g = sin(124°) * 100 * sin(21°)

h = sin(31°) * 100 * sin(19°)

Koordinatentransformation:

x_C = g cos 35°

y_C = g sin 35°

x_D = h cos 130°

y_D = h sin 130°

euklidische Distanz:

291,414 m

Answer 3

Die richtige Zeichnung sähe etwa so aus:

Dann wäre die Brücke mit Sicherheit länger als 232 m.