Trigonometrie 1, Berechnung von Seite und Höhe des gleichschenkligen Dreieck ABC mit a = b = 5cm ist cos (α) = 0,7.

Question

vielleicht könnte bitte jemand einen Blick über meine Rechnungen werfen?

Folgende Aufgabe: 

In einem gleichschenkligen Dreieck ABC mit a = b = 5cm ist cos (α) = 0,7. Berechne die Höhe h_c  und die Länge der Basis c.

cos (α) = 1/2 c  /  b = c / 2b    (das war leider nur geraten...)

c = cos (α) * 2b = 10cm * 0,7 = 7cm

a²   = h_c * + ( c/2 )²

h_c = √( 5² - 3,5² )

h_c = 3,6 cm

 

Vielen Dank an Euch und Grüße,

Sophie

Answer 1

Hallo Sophie :-)

so in etwa sieht das Dreieck aus:

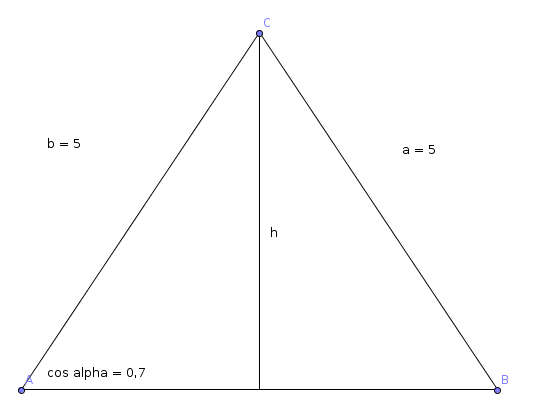
cos(α) = Ankathete/Hypotenuse = 0,7

Also

Ankathete = 0,7 * Hypotenuse = 0,7 * 5 = 3,5

Diese Ankathete ist die Hälfte von c, demnach ist c 7cm - richtig :-)

 

h kann man dann wie gewohnt mit Pythagoras berechnen:

3,5² + h² = 5²

h² = 25 - 12,25 = 12,75

h = √12,75 ≈ 3,57

Ja, sieht doch gut aus :-D

 

Liebe Grüße

Andreas

Comments

b = c/(2b) passt nicht.

Du meinst cos(a) = (1/2*c)/b

Das lässt sich wunderschön an der Skizze von Brucybabe erkennen :).

 

Hab sie mal modifiziert

Nun cos(a) = Ankathete/Hypotenuse = (c/2)/b = 0,7

Und (c/2)/b = (c/2)*(1/b) = c/(2b)

 

Alles klar? :)

---

@Andreas


Dickes Kompliment für die Zeichnung!

Damit konnte Inconnu zwei Fliegen mit einer Klappe schlagen und mir für diese Aufgabe die letzte Unsicherheit nehmen.

---

Avec plaisir!

Answer 2

Berechne die Höhe h_c  und die Länge der Basis c.

cos (α) =  (1/2 c)  /  b = c / (2b)    (das war leider nur geraten...)

Das stimmt aber schon.

 

a²   = h_c^2 + ( c/2 )²

h_c = √( 5² - 3,5² )

h_c = 3,571 cm

Comments

(1/2 c)  /  b

=  (1/2 *c/1)  /  (b/1) =

= (c /2) / (b/1)

= (c /2) * (1/b)

= c / (2b)

Answer 3

 

ist genau richtig ;). Zur Kontrolle kannst Du bei sowas ja auch eine Skizze machen ;).


Grüße