Kartenspiel und Glücksrad

Question

Aufgabe:

1.

Auf einem Tisch liegen vier Kreuzkarten und m Herz- bzw. Karokarten. Sie decken nun zwei Karten auf. Berechnen Sie den Wert von m, für den die Wahrscheinlichkeit dafür, dass genau eine Kreuzkarte unter den aufgedeckten Karten ist gleich ist.

2.

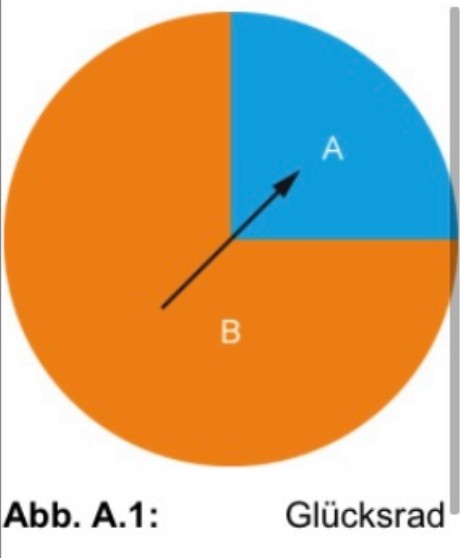
Das Glücksrad von Abb. A.1 wird zweimal gedreht. Es gilt \( p(\mathrm{A}) = 0,25 \).

a) Skizzieren Sie das Baumdiagramm zu diesem Zufallsversuch.

b) Berechnen Sie die Wahrscheinlichkeit für das Ereignis AA und für das Ereignis BB.

c) Begründen Sie, warum das Ergebnis B beim zweiten Drehen unabhängig vom Ergebnis des ersten Drehens ist.

Ich hoffe, es kann mir jemand helfen, dies zu berechnen.

Comments

unter den aufgedeckten Karten ist gleich ... ist.

Fehlt hier etwas?

Answer 1

2.a) AA,AB,BA,BB

b)P(AA) = (1/4)^2, P(BB) = (3/4)^2

c) Das Rad hat kein Gedächtnis. Die WKT ändern sich nach jedem Dreh nicht.

(Ziehen mit Zurücklegen)

Comments

Ich soll ein Baumdiagramm zeichnen . Wie soll ich das machen ?.. und vielen Dank für die Antwort

Answer 2

Hallo,

Aufgabe 1 sieht unvollständig aus.

Zu Aufgabe 2:

a) kannst du doch, oder?

b) P(AA)=0,25*0,25

  P(BB)=0,75*0,75

c) Was denkst du denn?

Comments

Also das ist die 1 Aufgabe

Auf einem Tisch liegen vier Kreuzkarten und m Herz- bzw. Karokarten. Sie decken nun zwei Karten auf. Berechnen Sie den Wert von m, für den die Wahrscheinlichkeit dafür, dass genau eine Kreuzkarte unter den aufgedeckten Karten ist gleich 2/5 ist.

---

Insgesamt sind es 4+m Karten.

Die Wahrscheinlichkeit, dass die 1. eine Kreuz-Karte ist, beträgt 4/(m+4). Die zweite Karte soll kein Kreuz sein: m/(m+3).

Nun multiplizieren:

4m/(m+4)(m+3)

Da es auch umgekehrt sein kann:

m/(m+4) * 4/(m+3)

Beide addieren und gleich 2/5 setzen:

8m/(m+4)(m+3) = 2/5

40m = 2(m+4)(m+3)

...

m=1 oder m=12

---

Dankeschön jetzt habe ich es verstanden !

---

Ich kriege es irgendwie nicht hin dass Baumdiagramm zu skizzieren

---

Das könnte so aussehen:

---

Vielen vielen Dank :)