Sekante, Tangente oder Passante?

Question

Aufgabe:

Sekante, Tangente oder Passante?

Problem/Ansatz:

F(x)=x²-2x+3

G(x)=2x-1

Bei dem Gleichsetzen soll 2 für x und 3 für y rauskommen, komme aber nicht darauf. Kann mir das jemand rechnen?

Comments

Kann mir das jemand rechnen?

Nein, denn es

soll 2 für x und 3 für y rauskommen

aber in den Gleichungen gibt es keine Variable y.

Answer 1

Aus x²-2x+3=2x-1 wird x²-4x+4=0.

Jetzt pq-Formel...

Answer 2

x²-2x+3 = 2x-1

<=>  x²-4x+4 = 0

<=>   (x-2)^2 = 0

<=>     x=2   also Tangente.

Answer 3

\(\begin{aligned} x^{2}-2x+3 & =2x-1\\ x^{2}-4x+4 & =0\\ x & =-\frac{-4}{2}\pm\sqrt{\left(\frac{-4}{2}\right)^{2}-4}=2\\ F(2) & =2^{2}-2\cdot2+3=3 \end{aligned}\)

Answer 4

Hallo,

\(x^2-2x+3=2x-1\quad|-2x,+1\\ x^2-4x+4=0\)

Jetzt kannst du beispielsweise mit der pq-Formel weiterrechnen und dein Ergebnis für x in eine der beiden Gleichungen einsetzen, um y zu berechnen.

Gruß, Silvia

Answer 5

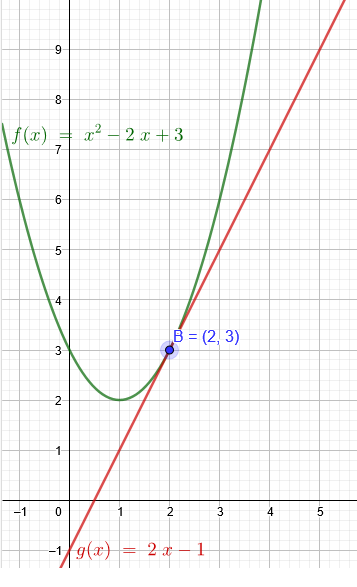
f(x)=x^2-2x+3

g(x)=2x-1

x^2-2x+3=2x-1|-2x

x^2-4x+3=-1|-3

x^2-4x=-4

(x-2)^2=-4+2^2=0|\( \sqrt{} \)

x-2=0

x=2  →  f(2)=2^2-2*2+3=3      g(2)=2*2-1=3

Es gibt nur einen gemeinsamen Punkt beim Schnitt von der Parabel und der Geraden.

Berührpunkt B(2|3)

Somit ist g(x) eine Tangente an die Parabel.