Aufgabe:
Bei dieser Aufgabe c) ist für b4 also die letzte Zahl 1, jedoch besteht letzte Zeile in der Matrix nur aus Nulleinträgen wodurch ich da auf 1=0 kam und das nicht richtig sein kann weshalb ich nicht mehr weiß wie ich da weiter machen soll.

Text erkannt:
Betrachten Sie die folgende Matrix in Zeilenstufenform:
\( \left(\begin{array}{ccccc} 2 & 1 & 4 & 0 & 8 \\ 0 & 0 & 2 & 5 & 5 \\ 0 & 0 & 0 & 3 & -3 \\ 0 & 0 & 0 & 0 & 0 \end{array}\right) \)
a) Bestimmen Sie \( \mathcal{L}_{0}(A) \).
b) Sei \( b=\left(\begin{array}{c}13 \\ 2 \\ -6 \\ 0\end{array}\right) \). Zeigen Sie, dass \( x_{0}=\left(\begin{array}{c}1 \\ -1 \\ 1 \\ -1 \\ 1\end{array}\right) \) eine Lösung des LGS \( A x=b \) ist. Bestimmen Sie alle Lösungen dieses LGS.
c) Sei \( b^{\prime}=\left(\begin{array}{l}1 \\ 0 \\ 0 \\ 1\end{array}\right) \). Bestimmen Sie alle Lösungen des LGS \( A x=b^{\prime} \).
Bei dieser Aufgabe weiß ich gar nicht wie ich anfangen soll vor allem bei der a) weiß ich nicht mit was ich anfangen soll.
Text erkannt:
a) Zeigen Sie, dass es für jede natürliche Zahl \( n \in \mathbb{N} \) eindeutige \( p, m \in \mathbb{N}_{0} \) gibt, so dass \( n=2^{p}(2 m+1) \)
b) Nutzen Sie a) um eine bijektive Abbildung in \( \mathrm{Abb}\left(\mathbb{N}, \mathbb{N}^{2}\right) \) zu konstruieren.
Problem/Ansatz:
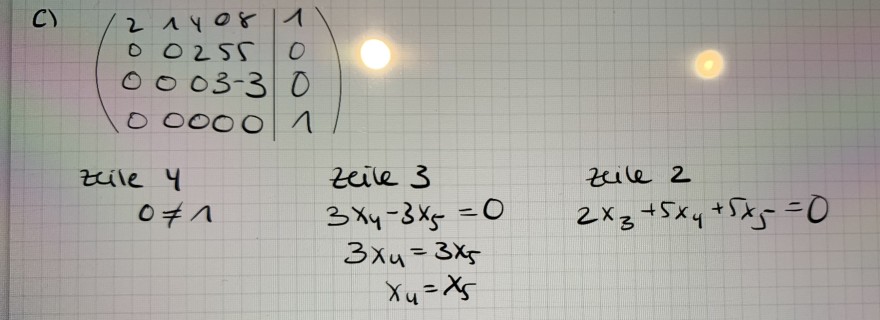
Text erkannt:
C) \( \left(\begin{array}{lll|l}2 & 1 & 4 & 08 & 1 \\ 0 & 0 & 255 & 0 \\ 0 & 0 & 03-3 & 0 \\ 0 & 0000 & 1\end{array}\right) \)
zile 4
\( \begin{array}{cc}0 \neq 1 & \text { zeile } 3 \\ 3 x_{4}-3 x_{5}=0 & 3 x_{4}=3 x_{5} \\ x_{4}=x_{5} & \text { zile } 2\end{array} \)