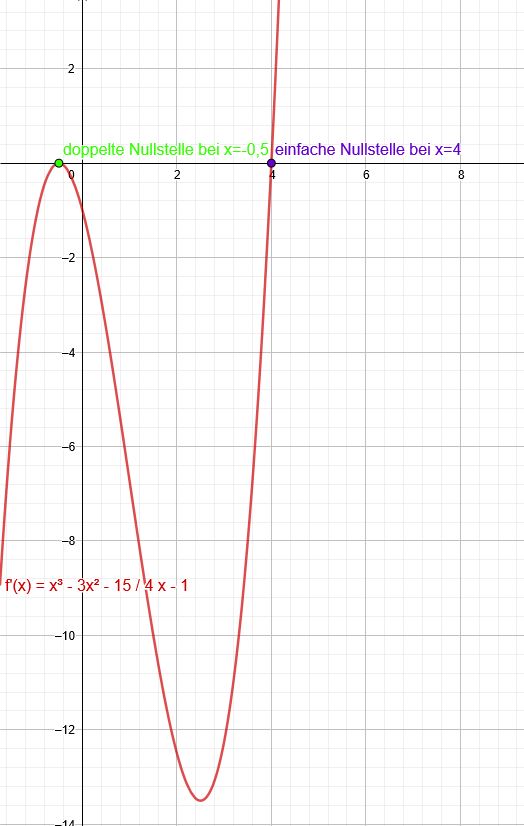
Nullstellen finden von:
\(f ' (x) = x^3 - 3x^2 - \frac{15}{4}x -1\)
\(f '' (x) = 3x^2 - 6x - \frac{15}{4}\)
\(3x^2 - 6x - \frac{15}{4}=0\)
\(x^2 - 2x - \frac{5}{4}=0\)
\(x^2 - 2x +\red{(\frac{2}{2})^2}=\frac{5}{4}+\red{(\frac{2}{2})^2}\) \(\red{ quadratische Ergänzung}\)
\(x^2 - 2x +1=\frac{5}{4}+1=\frac{9}{4}\) →2. Binom:
\((x-1)^2=\frac{9}{4} |\sqrt{~~}\)
1.)
\(x-1=\frac{3}{2} \)
\(x_1=1+\frac{3}{2} =2,5 \) \(f ' (2,5) = (2,5)^3 - 3\cdot (2,5)^2 - \frac{15}{4}\cdot (2,5) -1=-13,5\)
2.)
\(x-1=-\frac{3}{2} \)
\(x_2=1-\frac{3}{2} =-0,5 \) \(f ' (-0,5) = (-0,5)^3 - 3\cdot (-0,5)^2 - \frac{15}{4}\cdot (-0,5) -1=0\)
ist doppelte Nullstelle von \(f ' (x) \)