Beweis Injektivität und Surjektivität einer Abbildung

Question

Hallo,

Wie löse ich folgende Aufgabe:

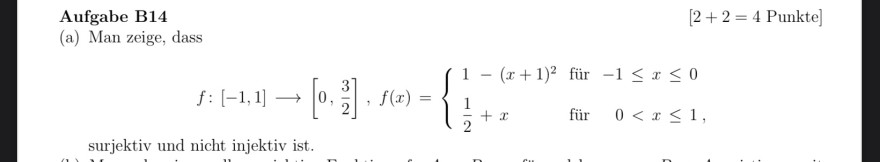
Text erkannt:

Aufgabe B14
\( [2+2=4 \) Punkte \( ] \)
(a) Man zeige, dass
\( f:[-1,1] \rightarrow\left[0, \frac{3}{2}\right], f(x)=\left\{\begin{array}{lll} 1-(x+1)^{2} & \text { für } & -1 \leq x \leq 0 \\ \frac{1}{2}+x & \text { für } & 0<x \leq 1 \end{array}\right. \)
surjektiv und nicht injektiv ist.

Um die fehlende Injektivität zu beweisen, habe ich Werte für x in die jeweils Funktion eingesetzt und habe z. B. für x=-1 und x=0,5 den Wert 1 rausbekommen. Reicht das in diesem Falle als Beweis aus?

Die Grundlegende Idee, was zu zeigen ist bei der Surjektivität ist mir klar, jedoch nicht der Ansatz bzw. der Weg. Könnte mir das jemand bitte erklären?

Und noch eine kleine weiter Frage: Wie nenne ich eine solche Funktion,die für unterschiedliche Intervalle aufgeteilt ist?

Answer 1

Aloha :)

$$f\colon[-1|1]\to\left[0\bigg|\frac32\right]\;,\;f(x)=\left\{\begin{array}{cl}1-(x+1)^2 &\text{für }-1\le x\le0\\[1ex]\frac12+x&\text{für }\phantom{+}0<x\le1\end{array}\right.$$

Surjektivität

Wir betrachten beide Funktionsterme getrennt.

1 Fall: \(-1\le x\le 0\)

Der Funktionsterm \(f(x)=1-(x+1)^2\) ist stetig. Nach dem Zwischenwertsatz nimmt die Funktion \(f\) jeden Funktionswert zwischen \(f(0)=0\) und \(f(-1)=1\) mindestens 1-mal an.

2. Fall: \(0<x\le1\)

Der Funktionsterm \(f(x)=\frac12+x\) ist stetig. Nach dem Zwischenwertsatz nimmt die Funktion \(f\) jeden Funktionswert zwischen \(f(\frac12)=1\) und \(f(1)=\frac32\) mindestens 1-mal an.

Beide Fälle zusammen garantieren, dass jedes Element aus der Zielmenge \([0|\frac32]\) mindestens 1-mal getroffen wird. Daher ist die Funktion surjektiv.

Injektivität

Es ist \(f(-1)=1\) und \(f(\frac12)=1\). Der Wert \(1\) aus der Zielmenge wird also mehr als 1-mal getroffen. Die Funktion \(f\) ist daher nicht injektiv.

Comments

Vielen Dank für die Hilfe. Und wie nennt man eine solche Funktion mit mehreren Funktionstermen für unterschiedliche Intervalle?

---

Ich kenne die Bezeichnungen "stückweise definierte Funktion" oder "abschnittweise definierte Funktion".