Berechnen Sie den Inhalt der Querschnittsfläche des Flusstals. Fläche berechnen, die Parabel und Sehne einschließen.

Question

Aufgabe 1:

Der Graph der Funktion \( f \) mit \( f(x)=-\frac{1}{8} x^{3}+\frac{3}{4} x^{2} \) beschreibt modellhaft das Profil eines Flusstals.
Bei Hochwasser kann das Wasser bis zum Hochpunkt des Graphen ansteigen. Berechnen Sie für diesen Fall den Inhalt der Querschnittsfläche des mit Wasser gefüllten Flusstals.

Aufgabe 2:

In die Normalparabel mit der Gleichung \( y=x^{2} \) ist eine Sehne mit den Endpunkten \( P_{1}\left(-1 \mid y_{1}\right) \) und \( P_{2}\left(2 \mid y_{2}\right) \) gezeichnet. Berechnen Sie den Flächeninhalt der Fläche, die Parabel und Sehne einschließen.

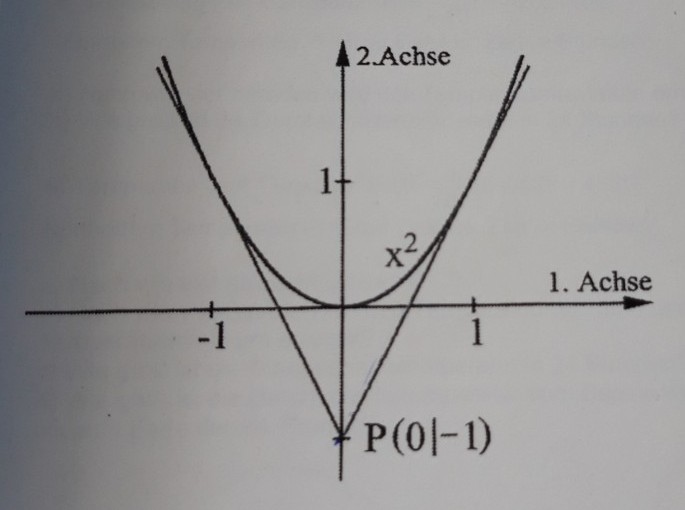
Aufgabe 3:

Vom Punkt \( P(0 \mid-1) \) sind die Tangenten an den Graphen der Funktion \( f \) mit \( f(x)=x^{2} \) gezeichnet. Berechnen Sie den Flächeninhalt der Fläche, die die Tangenten und der Graph miteinander einschließen.

Aufgabe 4:

Gegeben sind die Funktionen \( f \) mit \( f(x)=x^{2} \) (Graph ist die Normalparabel) und \( g \) mit \( g(x)=m \cdot x \) (Graph ist eine Ursprungsgerade).

Bestimmen Sie m, so dass der Flächeninhalt der Fläche, die von beiden Graphen eingeschlossen wird, \( \frac{4}{3} \) beträgt.

Answer 1

Ansätze mit Kontroll-Lösung:

f'(x) = 0 → x = 0 (TP) ∨ x = 4 (HP)

f(4) = 4

f(x) = 4 -->x = -2 ∨ x = 4

A = 6·4 - ∫ (- 2 bis 4) f(x) dx = 13.5 [korrigiert nach Kommentar]

Skizze:

Comments

Wie kommt man auf -2

---

f(x) = 4

Setz die Funktion gleich 4 und bestimme dann die Nullstellen von f(x) - 4. Du kannst das Horner Schema oder die Polynomdivision anwenden. Wenn du weißt das 4 sogar eine doppelte Nullstelle ist, kannst du das zweimal machen. Dann bleibt als Rest eine lineare Funktion deren Nullstelle recht einfach zu bestimmen ist.

Alternativ erlaubt der Lehrer vielleicht sogar das Lösen der kubischen Gleichung mittels Taschenrechnereinsatz oder ganz normaler Wertetabelle.

---

Aber warum eig nicht das integral von 0 bis 4

---

Es geht um die oben von mir skizzierte Fläche. und du siehst doch auch noch die Fläche auf der linken Seite der y-Achse also für negative x-Werte.

---

I(- 2 bis 4) f(x) dx = 10.5

das ist NICHT die gesuchte Fläche aus der Zeichnung oben! Besser$$A = \int\limits_{-2}^4 4-f(x)\,\text dx = 13,5$$

---

Die Skizze kann ich nachvollziehen aber in der aufgabe steht doch kann das Wasser bis zum hochpunkt des Graphen steigen. Da denk ich es beginnt ab Null

---

Da denk ich es beginnt ab Null

Es beginnt in vertikaler Richtung an der tiefsten Stelle des Profils, also bei 0. Das spielt aber überhaupt keine Rolle.

Die Integration läuft in horizontaler Richtung, also in X-Richtung. Und der am weitest links liegende Punkt der gesuchten Fläche liegt bei \(x=-2\) (s. Skizze oben). Integriert wird bis \(x=4\), was zufällig der gleiche Wert ist, wie der Hochpunkt bei \((x=4|\,y=4)\). Ergo ist die gesuchte Fläche \(A\):$$A = \int\limits_{{\color{red}\boldsymbol{x}}=-2}^{{\color{red}\boldsymbol{x}}=4} 4-f(x)\,\text dx = 13,5$$

---

Danke Werner für die Korrektur. Ich habe das in der Lösung berichtigt.

Answer 2

Bei 1 sieht das erst mal so aus:

~plot~ -x^3/8+3x^2/4 ~plot~

Die Fläche kannst du dann mit einem geeigneten

Integral ausrechnen.

Comments

Danke schön. Und wie sieht es bei 2 aus ich habe ja keine vollständigen Punkte gegeben

---

Bei Aufgabe 2) sind die beide Punkte angegeben, die x-Koordinaten mit einer Zahl und die y-Koordinaten mit einer Formel.

---

Aber du hast die Funktionsgleichung. Wenn du da das x einsetzt

kannst du die y-Werte ausrechnen.

---

Und die Formel lautet wie

---

Steht doch bei 2:    y=x^2  bzw. f(x)=x^2.

---

Und die Formel lautet wie

Willst Du uns verkohlen? Wenn dort steht y = x^2, dann ist wahrscheinlich gemeint, dass y = x^2

Answer 3

Hallo,

zu Aufgabe 2

Bestimme die y-Koordinaten der beiden Punkte und stelle die Gleichung der Geraden auf, die durch diese beiden Punkte geht. Berechne dann den Flächeninhalt zwischen Gerade und Parabel.

zu 3)

Stelle die Gleichung der Geraden durch P und den Punkt durch (1|1) auf. Berechne das Integral zwischen Gerade und Parabel von 0 bis 1 und verdopple es.

zu 4)

Bestimme die Schnittstelle von f(x) und g(x) = obere Grenze des Integrals und bestimme den Flächeninhalt zwischen Graph und Parabel in Abhängigkeit von m. Setze dein Ergebnis = 4/3 und löse nach m auf.

Gruß, Silvia