Bestimmen Sie den Inhalt der Querschnittsfläche des Rotationskolben (gelbe fläche)

Question

Aufgabe:

a) Modellieren Sie die obere Randkuve des abgebildeten Rotationdkolbens durch eine quadratische Funktion.

b) Bestimmen Sie den Inhalt der Querschnittsfläche des Rotationskolben (gelbe fläche)

Problem/Ansatz:

Hab bei der a) f(x)= -1/18x^2+2/3x

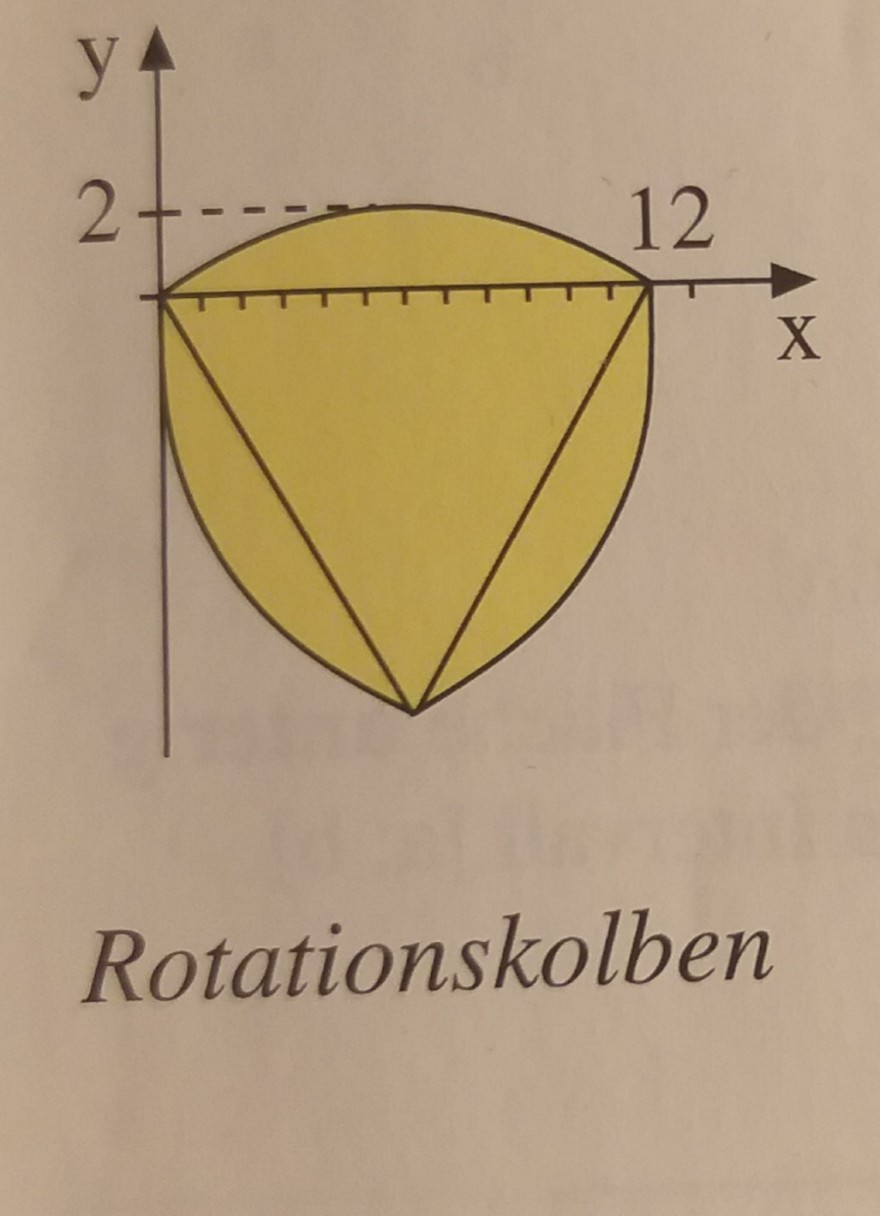
Bei der b) hab ich die Idee gehabt, dass Integral von f(x) von 0 bis 12 mal 3 zu nehmen und dann vom gleichseitigen Dreick die Fläche zu berechnen. Ich habe insgesamt 110,3538 FE raus. Bin mir aber unsicher.

Text erkannt:

Rotationskolben

Answer 1

a) Das ist eine Parabel mit Scheitel (6;2) also

y = a*(x-6)^2 + 2

Einsetzen von (0;0) ergibt a= -1/18

b) Bei der Fläche habe ich auch das gleiche raus.

Comments

Ja das hab ich auch gesehen und bin mir ziemlich sicher, dass die ich die a) richtig habe, bin mir bei der b) nicht so sicher.

---

Wenn mathef bei b) das gleiche Ergebnis wie du hat, kannst du dir sicher sein, dass es richtig ist.

---

Ich hatte für das Integral 16 und für das Dreieck gemäß

a^2/4 *√3 was hier auf 36√3 führt.

Insgesamt also 3*16+ 36√3 = 48+ 36√3≈110,354

---

Hallo mathef,
die 3 " Parabelflächen " könnten auch
" Kreissegmente sein "
Eine Recherche im Internet legt das nahe,
aber auch nicht mit 100 % Sicherheit.

---

Laut Aufgabe a hier aber Parabeln.

Nach Wikipedia https://de.wikipedia.org/wiki/Wankelmotor#Geometrie

war es zumindest beim Herrn Wankel noch was anderes.

---

Richtig.
quadratische Funktion hatte ich
übesehen.