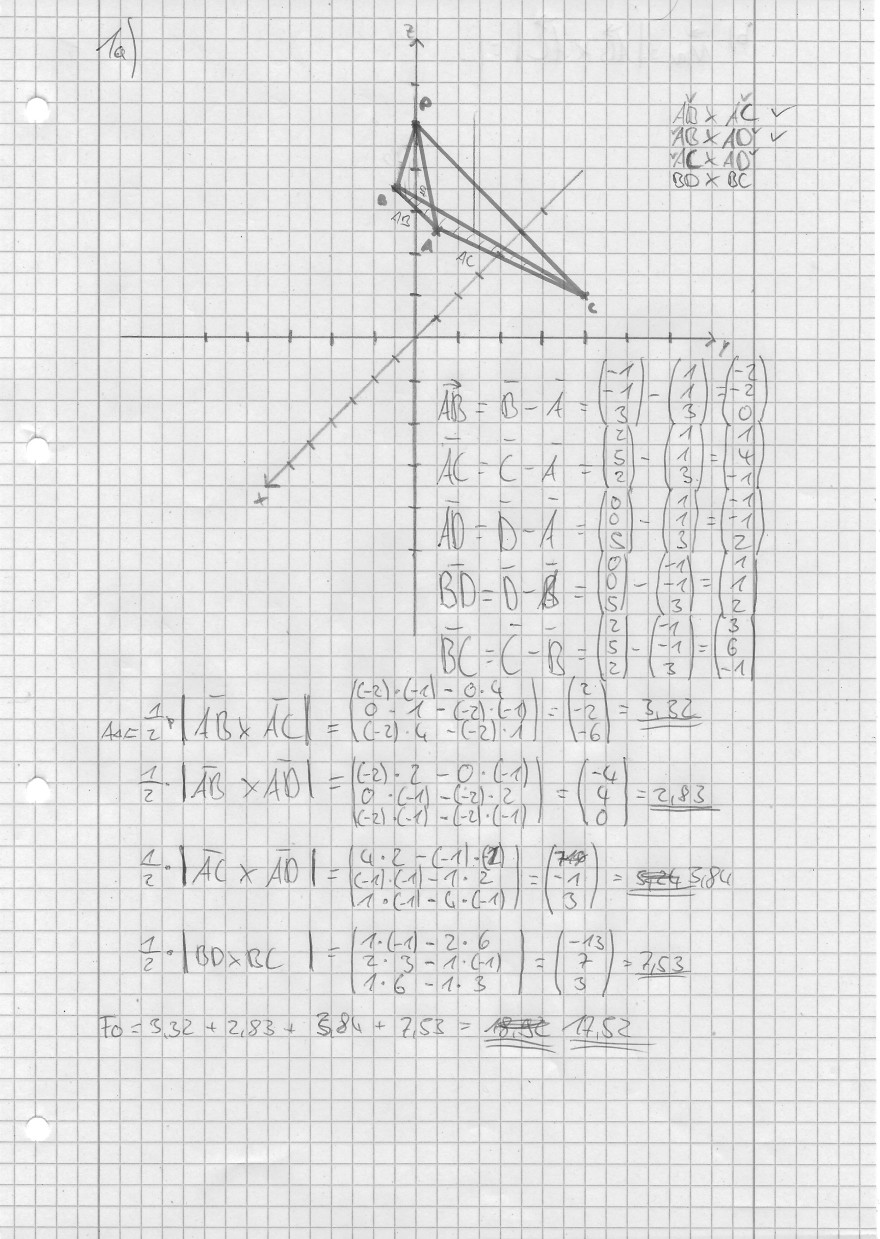
Könnte jemand mal über meine Rechnung dieser 3 Vektorrechnungen drüber schauen?
Bin mir absolut unsicher ob die Vorgehensweise so richtig ist. Aber mir würde jetzt nichts anderes einfallen. Danke im Voraus. Es geht um die Aufgaben 1a bis c.
Und falls jemand bei der 1d helfen kann wäre ich auch sehr dankbar weils mir immernoch nicht schlüssig ist.
Aufgabe
1. Gegeben ist ein kartesisches Koordinatensystem \( \Sigma \) und die \( \mathrm{Punkte} \mathrm{A}(1|1| 3), \mathrm{B}(-1|-1| 3), \mathrm{C}(2|5| 2) \) und \( \mathrm{D}(0|0| 5) \). Die Punkte A bis D sind die Eckpunkte einer Dreieckspyramide.
(a) Berechnen Sie den Oberflächeninhalt der Dreieckspyramide.
(b) Berechnen Sie zwei Vektoren \( \vec{N}_{A B C} \) und \( \vec{N}_{A B D} \), die senkrecht auf den Flächen \( \mathrm{ABC} \) bzw. \( \mathrm{ABD} \) stehen.
(c) Berechnen Sie den Winkel, den \( \vec{N}_{A B C} \) und \( \vec{N}_{A B D} \) einschließen und den Winkel zwischen \( \vec{N}_{A B C} \) und \( \overrightarrow{A D} \).
(d) Die Vektoren \( \vec{A}, \vec{B} \) und \( \vec{C} \) bilden das Basissystem b. Geben Sie die Eckpunkte der Pyramide in diesem Basissystem an.
(e) Geben Sie die Gleichung der Geraden an, die senkrecht zur Seite ABC ist und durch den Punkt D geht.