Green-Funktion für Polarkoordinaten
Ich möchte die folgende Aufgabe lösen:
Text erkannt:
Gegeben ist eine homogene Linienladungsdichte \( \rho_{\mathrm{L}} \) im Vakuum entlang der \( z \)-Achse. Ohne Randbedingungen im Endlichen und unter Beachtung der Translationsinvarianz in \( z \) Richtung reduziert sich die Berechnung der Greenschen Funktion für das elektrische Potential auf ein zweidimensionales Problem in \( \operatorname{der} \rho-\varphi \)-Ebene.
Bestimmen Sie die Greensche-Funktion dieses zweidimensionalen Problems ohne Randbedingungen im Endlichen. Betrachten Sie hierfür die Poisson-Gleichung in der Ebene und nutzen Sie zur Lösung den Gaußschen Satz in diesen zwei Dimensionen.
Hier gehts zwar um Theoretische Elektrotechnik, aber eine Poisson-Gleichung mit einer Green-Funktion zu lösen, ist ja zunächst ein mathematisches Problem.
Was ich schon versucht habe:
Ich habe die Green-Funktion für den eindimensionalen Fall gesucht. Diese muss die Gleichung
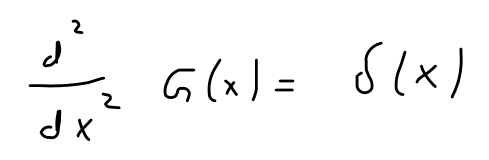
Text erkannt:
\( \frac{d^{2}}{d x^{2}} G(x)=\delta(x) \)
erfüllen, wobei delta die Delta-Distribution ist. Diese Aufgabe habe ich zeichnerisch gelöst, indem ich die Delta-Distribution zweimal aufgeleitet habe:
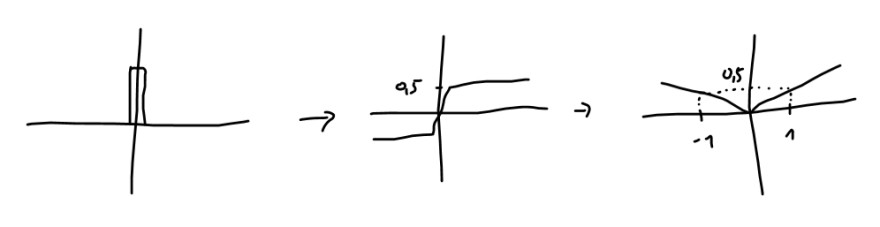
Das Ergebnis ist
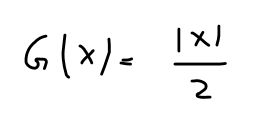
Text erkannt:
\( G(x)=\frac{|x|}{2} \)
Jetzt aber haben wir die vorliegende Aufgabe, in der wir den zweidimensionalen Fall mit Polarkoordinaten haben. Keine Ahnung, was hier zu tun ist. Wer kann helfen?
Die gesuchte Lösung ist
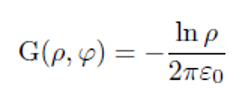
Text erkannt:
\( \mathrm{G}(\rho, \varphi)=-\frac{\ln \rho}{2 \pi \varepsilon_{0}} \)