Untersuche Folge auf Konvergenz

Question

Ich untersuche die folgende Folge auf Konvergenz:

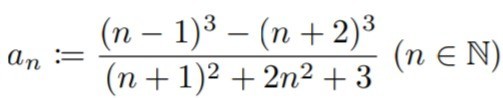
Text erkannt:

\( a_{n}:=\frac{(n-1)^{3}-(n+2)^{3}}{(n+1)^{2}+2 n^{2}+3}(n \in \mathbb{N}) \)

a_n = \( \frac{-9*n^2 - 9*n - 9}{3*n^2 +2*n +4} \)

Behauptung: a_n konvergiert gegen -3

zu zeigen: Für alle ε >0 gilt n = |an - a| <ε für fast alle n

Beweis:

| \( \frac{-9*n^2 - 9*n - 9}{3*n^2 +2*n +4} \) - (-3) | < ε

| \( \frac{-3*n + 3}{3*n^2 + 2*n + 4} \) | < ε

\( \frac{3*n - 3}{3*n^2 + 2*n + 4} \) < ε

Wie macht man weiter?

Answer 1

a(n) = ((n - 1)^3 - (n + 2)^3) / ((n + 1)^2 + 2·n^2 + 3)

a(n) = (- 9·n^2 - 9·n - 9)/(3·n^2 + 2·n + 4)

lim n → unendlich

a(n) = (- 9)/(3) = - 3

Die Vereinfachung des Termes hilft auch bei der Epsilon-Umgebung.

Comments

In der Aufgabe steht, dass wir die Folge auf Konvergenz untersuchen und ggf den Grenzwert angeben sollen.

Am Ende muss man aber ein n₀ finden , für n₀ > ...ε  gilt |a_n - (-3) | < ε , oder?

---

Eigentlich brauchst du nur den Grenzwert zu beweisen, damit weißt du dann doch auch um zu zeigen das fast alle Werte in dieser Y-Umgebung liegen. Dazu brauchst du nicht für ein beliebiges Epsilon ein n berechnen.