Für welche a E R ist f stetig?

Question

Aufgabe:

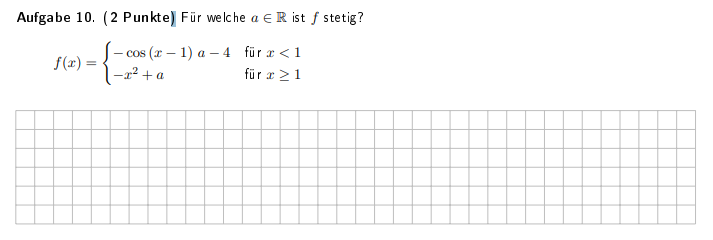
Text erkannt:

Für welche \( a \in \mathbb{R} \) ist \( f \) stetig?
\( f(x)=\left\{\begin{array}{ll} -\cos (x-1) a-4 & \text { für } x<1 \\ -x^{2}+a & \text { fü } r \geq 1 \end{array}\right. \)

Problem/Ansatz:

Ich habe versucht es gleichzusetzen, aber das in beiden ein a steht verwirrt mich. Mir ist klar das ich a brauch und somit die Gleichung der Stetigkeitsbedingung erfüllen muss. Die Lösung habe ich auch, allerdings versteh ich nicht ganz was gemacht wurde. Lösung ohne Rechenweg ist nicht ganz hilfreich. Wäre mega wenn mir jemand das erklären könnte.

Text erkannt:

Für welche \( a \in \mathbb{R} \) ist \( f \) stetig?
\( f(x)=\left\{\begin{array}{ll} -\cos (x-1) a-4 & \text { für } x<1 \\ -x^{2}+a & \text { fü } r \geq 1 \end{array}\right. \)

Answer 1

- cos ( x-1) * a - 4
x^2 + a

Für x = 1

- cos ( 1-1) * a - 4
1^2 + a

-1 * a - 4 = 1 + a
- 4 - 1 = 2a
a = -2.5

Überprüfe das Ergebnis mit x = 1 und a = -2.5
Funktionswert für beide Gleichungen   -1.5