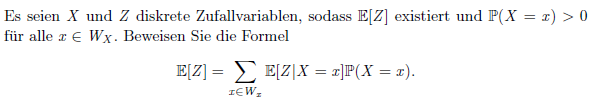
Text erkannt:
Es seien \( X \) und \( Z \) diskrete Zufallvariablen, sodass \( \mathbb{E}[Z] \) existiert und \( \mathbb{P}(X=x)>0 \) für alle \( x \in W_{X} \). Beweisen Sie die Formel
\( \mathbb{E}[Z]=\sum \limits_{x \in W_{x}} \mathbb{E}[Z \mid X=x] \mathbb{P}(X=x) \)
Sie können diese Formel benutzen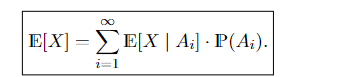
zu beweisen.Ai ist eine disjunkte Zerlegung von Ω.
Text erkannt:
\( \mathrm{E}[X]=\sum \limits_{i=1}^{\infty} \mathrm{E}\left[X \mid A_{i}\right] \cdot \mathbb{P}\left(A_{i}\right) \)
