Welcher/n Aussage(n) stimmen Sie für obige Mengen zu?

Question

Text erkannt:

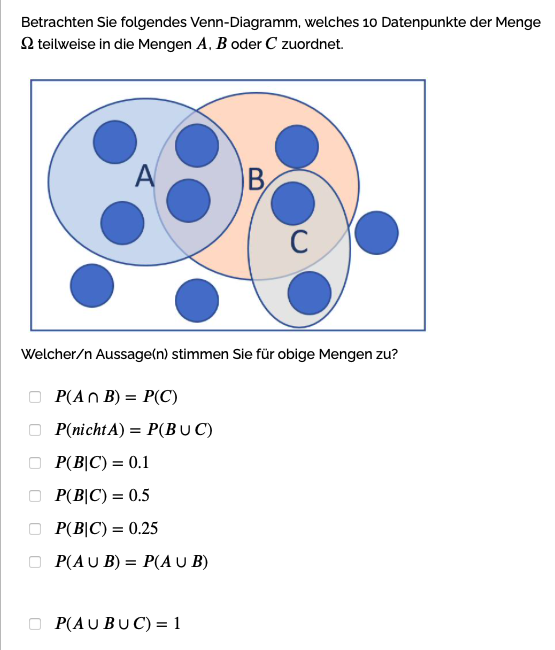
Betrachten Sie folgendes Venn-Diagramm, welches 10 Datenpunkte der Menge \( \Omega \) teilweise in die Mengen \( A, B \) oder \( C \) zuordnet.
Welcher/n Aussage(n) stimmen Sie für obige Mengen zu?
\( P(A \cap B)=P(C) \)
\( P( \) nicht \( A)=P(B \cup C) \)
\( P(B \mid C)=0.1 \)
\( P(B \mid C)=0.5 \)
\( P(B \mid C)=0.25 \)
\( P(A \cup B)=P(A \cup B) \)
\( P(A \cup B \cup C)=1 \)

Problem:

Kann mir hier jemand erklären weshalb unter anderem P(B/C) = 0.5 richtig ist? Wie komme ich hier auf diesen Wert?

Korrekt ist zusätzlich die 1 und die 6.

Aber wie erkenne ich das in der Abbildung. Werde hier nicht schlau. Vielen Dank.

Answer 1

Kann mir hier jemand erklären weshalb unter anderem P(B/C) = 0.5 richtig

Zwei Datenpunkte liegen in C. Davon gehört einer auch zu B.

In A∩B liegen 2 der 10 Datenpunkte. In C auch, also ist in beiden Fällen p=0,2.

Fragst du ernsthaft, warum der 6. Vorschlag richtig ist?

Comments

Danke.

Nein mir war nur die 0.5 nicht klar.