Gibt es einen Unterschied zwischen "Doppelstreifen" und "einfache Streifen"?

Question

Aufgabe:

Text erkannt:

Aufgabe 2: Berechnen Sie die folgenden Integrale näherungsweise nach Simpson:
a) \( \int \limits_{1}^{4} \sqrt{1+2 t^{4}} d t, n=10 \) (10 Doppelstreifen)
b) \( \int \limits_{0,5}^{1} \frac{x^{3}}{e^{x}-1} d x, n=5 \) (5 Doppelstreifen)
c) \( \int \limits_{1}^{3} \frac{e^{x}}{x^{2}} d x, n=5 \) (5 Doppelstreifen)

Problem/Ansatz:

Gibt es einen Unterschied zwischen "Doppelstreifen" und "einfache Streifen"? Verändert es bei der SImpsonregel irgendwas, wenn da Doppelstreifen stehen? Oder schreibt man trotzdem (b-a)/3n ?

Danke :)

Answer 1

Bei der Simpson Regel wird ein Integrationsintervall $$ [x_i , x_{i+1} ] $$ immer in zwei Streifen zerlegt. Das erste ist $$ \left[ x_i , \frac{x_i + x_{i+1}}{2} \right] $$ und das zweite $$ \left[ \frac{x_i + x_{i+1}}{2} , x_{i+1} \right] $$

Somit gibt es meiner Meinung nach immer nur Doppelstreifen und keine einfachen Streifen.

Für Aufgabe (a) habe ich eine Lösung beigelget.

Comments

Dankeschön :)
Wofür braucht man hier aber die Streifenanzahl? Wo setzt man diese ein bzw. was rechnet man damit?

---

Aus dem obigen Programm kannst Du ersehen, dass das Integrationsintervall von \( [ 1 , 4 ] \) in 10 Doppelstreifen aufgeteilt wird. Dadurch wird die Genauigkeit der numerischen Integration erhöht, weil die quadratische Anpassung, die bei der Simpsionregel verwendet wird, sich jeweils auf einen Doppelstreifen bezieht. Je schmaler er ist desto genauer die Approximation. Und die Doppelstrifen werden schmaler, wenn Du mehr berücksichtigst. Ist ja klar, weil das Integrationsintervall ja fix bleibt.

Siehe hier ein Doppelstreifen.

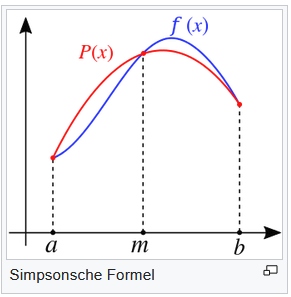هُ

Je mehr Doppelstreifen für das Integrationsintervall verwendet werden, desto genauer ist die Integration.