a_n := (( \frac{n+(-1)^n}{n} )^n für gerade n € N gegen 2.72 konvergiert bzw für ungerade n gegen 0.37?

Question

Wie kann man zeigen, dass die Folge

a_n := (\( \frac{n+(-1)^n}{n} \))ⁿ für gerade n € N gegen 2.72 konvergiert bzw. für ungerade n gegen 0.37 ?

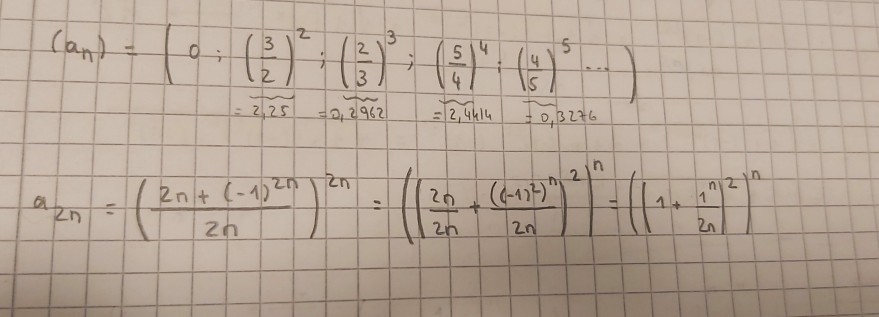
Text erkannt:

\( \left(a_{n}\right)=\left(0 ;\left(\frac{3}{2}\right)^{2} ;\left(\frac{2}{3}\right)^{3} ;\left(\frac{5}{4}\right)^{4} ;\left(\frac{4}{5}\right)^{5} \ldots\right) \)
\( =\sqrt{2,25}=0,2962=\sqrt{2,4414}=0,3276  \)
\( \left.a_{2 n}=\left(\frac{2 n+(-1)^{2 n}}{2 n}\right)^{2 n}=\left(\left(\frac{2 n}{2 n}+\frac{\left((-1)^{2}\right)^{n}}{2 n}\right)^{2}\right)^{n}\left(\mid 1+\frac{1^{n}}{2 n}\right)^{2}\right)^{n} \)

Comments

a_n := (\( \frac{n+(-1)^n}{n} \))n für gerade n € N gegen 2.72 konvergiert bzw. für ungerade n gegen 0.37 ?

Das kann man gar nicht zeigen. Es lässt sich vielmehr nachweisen, dass 2,72 bzw. 0,37 NICHT die gesuchten Grenzwerte sind.

Welcher Stümper hat diese Aufgabe verbrochen?

Answer 1

Aloha :)

Für gerade \(n\) lautet die Folge:$$a_n=\frac{n+1}{n}=\left(\frac nn+\frac1n\right)=\left(1+\frac1n\right)^n$$Für ungerade \(n\) lautet die Folge:$$a_n=\frac{n-1}{n}=\left(\frac nn-\frac1n\right)=\left(1-\frac1n\right)^n$$Das kannst du mit dem folgenden bekannten Grenzwert vergleichen:$$\lim\limits_{n\to\infty}\left(1+\frac xn\right)^n=e^x$$und stellst fest, dass unsere Folge für gerade \(n\) gegen \(e^1=e\) und für ungerade \(n\) gegen \(e^{-1}=\frac1e\) konvergiert.

Comments

Sind e und \( \frac{1}{e} \) auch Häufungswerte von a_n ?

---

Ja... es gibt 2 konvergente Teilfogen, eine für gerade n und eine für ungerade n. Die Grenzwerte dieser konvergenten Teilfogen sind Häufungspunkte.

---

\( \lim\limits_{n\to\infty} \) inf a_n =0

und Supremum existiert nicht , richtig?