Vektor gesucht stumpfer Winkel

Question

Text erkannt:

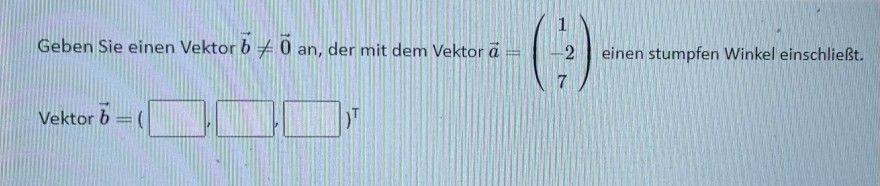
Geben Sie einen Vektor \( \vec{b} \neq \overrightarrow{0} \) an, der mit dem Vektor \( \vec{a}=\left(\begin{array}{c}1 \\ -2 \\ 7\end{array}\right) \) einen stumpfen Winkel einschließt. Vektor \( \vec{b}= \)

Text erkannt:

Geben Sie einen Vektor \( \vec{b} \neq \overrightarrow{0} \) an, der mit dem Vektor \( \vec{a}=\left(\begin{array}{c}1 \\ -2 \\ 7\end{array}\right) \) einen stumpfen Winkel einschließt. Vektor \( \vec{b}= \)

Hallo zusammen,

oben ist ein Bild von der Aufgabenstellung und ich weiß nicht wie man sie löst. Es ist nur ein Vektor gegeben und ich weiß, dass ein stumpfer Winkel > 90 grad und < 180 grad ist.

Würde mich freuen wenn mir jemand weiterhelfen könnte.

Answer 1

Das Skalarprodukt braucht nur negativ sein. Also z.B. [0, 1, 0]

Comments

Könntest du mir auch eine Erklärung geben damit ich das nachvollziehen kann? =)

---

Ist das Skalarprodukt zweier Vektoren Null bilden sie einen rechten Winkel.

Ist das Skalarprodukt zweier Vektoren > 0 bilden sie einen spitzen Winkel.

Ist das Skalarprodukt zweier Vektoren < 0 bilden sie einen stumpfen Winkel.

Das kannst du selber über die Definition des Skalarproduktes herleiten

$$\overrightarrow a \cdot \overrightarrow b = |\overrightarrow a| \cdot |\overrightarrow b| \cdot cos(\gamma)$$

Frage dich für welche Winkel der Kosinus größer, kleiner oder gleich Null ist.

---

Alles klar vielen Dank!

---

Könntest du mir auch eine Erklärung geben damit ich das nachvollziehen kann? =)

mache Dir ein Bild:

(klick auf das Bild)

Der gelbe Winkel zwischen den Vektoren$$\vec a = \begin{pmatrix}1\\ -2\\ 7\end{pmatrix}, \quad \vec b = \begin{pmatrix}0\\ 1\\ 0\end{pmatrix}$$ist größer als 90° und somit ein stumpfer WInkel.

---

Vielen Dank!