Hallo zusammen, ich bin mir nicht sicher ob ich die Aufgabe richtig gelöst habe, da ich normalerweise Probleme bei dieser speziellen Aufgabenstellung habe, wäre daher dankbar, wenn einer von euch das kontrolliert. Die Aufgabenstellung und meine Begründungen sind unterangegeben, Grüße und Dank für zukünftige Antworten.
Gegeben ist der Graph der Ableitungsfunktion \( f \) ' einer Funktion \( f \).
Geben Sie auch jeweils eine Begründung an.
a) Bestimmen Sie die Extremstellen von f.
b) Für welche \( x \)-Werte ist der Graph von \( f \) rechtsgekrümmt?
c) In welchem Bereich ist der Graph von \( f \) monoton fallend?
d) Überprüfen Sie die Aussage: \( f(0)<f(2) \).
e) An welchen Stellen ist der Graph von \( f \) parallel zur Geraden \( y=-4 x-2 ? \)
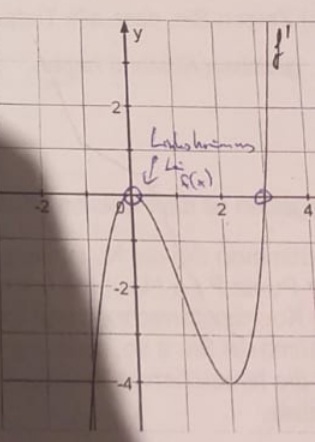
Zu a) Extremstellen sind bei der ersten Ableitung die Nullstellen, also wären das hier die Stelle 0 und 3, allerdings bin ich mir bei 0 nicht sicher, ob es eine ist, da sie ja eine Berührstelle ist und keine VZW aufzeigt.
Zu b) Eine Rechtskrümmung ist ein VZW der Wendepunkt, von + nach- bzw. Der Extremstellen der ersten Ableitung, allerdings gibt es glaub ich keine Rechts links kurve, da der Stelle 0 es von negativ nach negativ geht und bei der zweiten Stelle es von- nach + aber nie von + nach-, also gibt es keine oder?
Zu c) Die Funktion ist ja durchgehend unter der x-Achse zumindest bis zu P (3|0) also ist sie von -Unendlich bis 3 monoton fallend.
Zu d) Ist falsch, da die Funktion in diesem Intervall fallend ist und 2 niedrigere Funktionswerte als 0 hat.
Zu e) Wenn f zu dieser Gerade parallel ist, dann wäre f' auch zu y' parallel y' wäre dann -4 und wäre somit zu den Wendepunkte parallel also zu den Stellen 2 und 0.