Teilen durch "x" in Gleichungen / Vielfachheiten von Nullstellen

Question

Liebe Lounge,

ich habe eine Frage an euch. Und zwar geht es darum, ob und vor allem WIE man durch "x", also durch eine Variable teilen kann/darf. An dieser Stelle sei erwähnt, dass der Weg über das Ausklammern von x und dem "Nullproduktsatz" hier explizit nicht verwendet werden soll.

Dazu soll die folgende Gleichung gelöst werden (Lösungen sind: x1=0; x2=0 und x3=-1):

I. x³ = -x²

Wenn mann sich nun einmal die die zugehörigen Funktionen zu beiden Seiten der Gleichung anschaut, erkennt man folgendes:

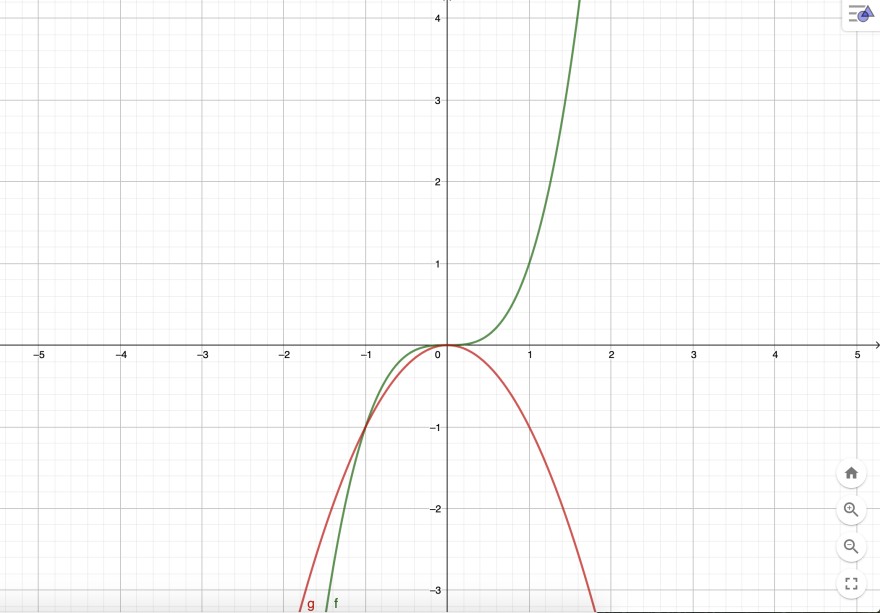
Generell gilt: Wenn zwei Funktionen an einer Stelle x den gleichen Funktionswert haben (und ebendiese Stellen suchen wir ja durch das Lösen der Gleichung), dann haben auch die Funktionen "geteilt durch den jeweiligen x-Wert" den gleichen Funktionswert. Da man allerdings nicht durch "0" teilen darf gilt die folgende Gleichung nur für x ungleich 0 (Die Stelle x=0 wird gesondert betrachtet. Daraus folgt: x1=0 als erste Lösung der Gleichung).

II. x²= -x

Betrachtet man wieder die zugehörigen Funktionsgraphen fällt nun aber auf, dass auch die "durch x geteilten Funktionsterme" einen gemeinsamen y-Wert an der Stelle 0 haben.

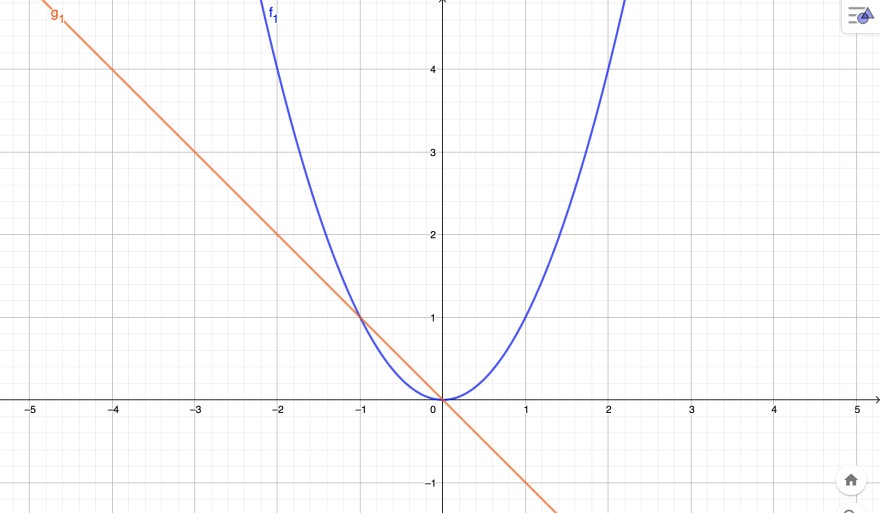
Wiederholt man das "Teilen durch x" ein weiteres Mal (wieder, nur möglich, für x ungleich 0) folgt die Gleichung:

III. x=-1 (welches die dritte Lösung der Gleichung war).

Was mir allerdings Kopfzerbrechen bereitet, ist das Folgende:

Bevor man Gleichung II durch x ungleich 0 teilt, sollte man ja wieder überprüfen, was an der Stelle x=0 gilt. Daraus folgt, dass auch in Gleichung II x=0 eine Lösung ist (vgl. x2 aus der Eingangsbeschreibung).

Dürfte man aber Strenggenommen in Gleichung II 0 gar nicht für x einsetzen? Sprich: Eigentlich haben die Funktionen aus Gleichung 2 (durch das vorherige Teilen durch x) doch an der Stelle x=0 eine Definitionslücke - oder?

Fest steht aber auch, dass 0 auch in Gleichung II eine Lösung ist. Demnach ist x=0 eine doppelte Nullstelle. Wie passt das aber mit der eigentlichen Definitionslücke zusammen?

Ich hoffe, meine Frage ist deutlich genug formuliert.

Ich danke für eure Hilfe!

Beste Grüße

Kombi

Comments

Falls du das einem Nachhilfeschüler beibringen willst, dürfte der überfordert sein, da Fallunterscheidungen als viel verwirrender wahrgenommen werden als das Nullprodukt.

Answer 1

Bei so viel Text finde ich deine Frage nicht. Zerlege den Lösungsweg in die Fälle (1) x²=0 und (2) x²≠0. Im Falle (1) erhältst du x=0, in Falle (2)  erhältst du x=-1.

Answer 2

Hallo,

x³ = - x²

wenn du die Gleichung durch x² teilen willst, kannst du einfach eine Fallunterscheidung machen:

1. Fall: x≠0      (und damit x² ≠ 0)

x = -1

2. Fall: x = 0

0 = 0  die Gleichung ist für x=0  allgemeingültig

----

[ x ≠ 0  und x = -1 ]    oder   x = 0

L = {0 , -1}

Gruß Wolfgang

Answer 3

Es geht bei der Bestimmung der Lösungen um den korrekten Gebrauch

äquivalenter logischer Umformungen:

\(x^3=-x^2\iff (x\neq 0\wedge x^3=-x^2)\vee (x=0\wedge x^3=-x^2)\).

Nun gilt (wie man mittels Division durch \(x^2\neq 0\) sieht):

\(x\neq 0\wedge x^3=-x^2\iff x\neq 0 \wedge x=-1\iff x=-1\) und

\(x=0\wedge x^3=-x^2\iff x=0\), insgesamt also

\(x^3=-x^2\iff (x=-1)\vee (x=0)\).

Answer 4

Hallo,

Was mir allerdings Kopfzerbrechen bereitet, ist das Folgende:

Bevor man Gleichung II durch x ungleich 0 teilt, sollte man ja wieder überprüfen, was an der Stelle x=0 gilt. Daraus folgt, dass auch in Gleichung II x=0 eine Lösung ist

Deshalb ist x=0 ja eine doppelte Nullstelle.

:-)

Comments

Ja, das ist schon klar. Aber bedeutet das, dass man nach dem Teilen durch x eigentlich zwar nicht mehr x einsetzen darf (Definitionslücke), die Funktionen die links und recht stehen aber eben trotzdem bei 0 den gleichen Funktionswert haben=

---

Du könntest gleich durch x^2 dividieren.

Ich finde ja, dass durch x zu teilen nur zu Verwirrung führt. Also lieber ausklammern und Nullprodukt.