Hallo Dennis,
Ich soll zeigen, dass \(\cos(2x)=1-2\sin^2(x)\) stimmt. ich weiß leider nicht wie
z.B. geometrisch am Einheitskreis. Der Kreis um \(O\) mit Radius \(|OT|=1\) soll ein Einheitskreis sein.
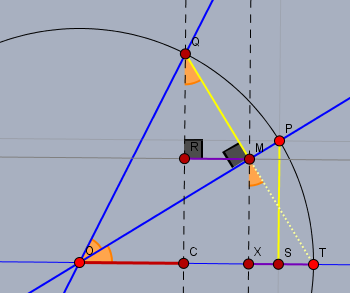
Der Winkel \(x\) ist jeweils orange markiert. $$\sin(x) = \frac{|SP|}{|OP|} = |SP| \\ \cos(2x) = \frac{|OC|}{|OQ|} = |OC|$$
Die Dreiecke \(\triangle OSP\) und \(\triangle OTM\) sind kongruent. Daraus folgt, dass \(|MT|=|SP|\) (gelb). Wegen der Symmetrie zur Geraden durch \(OP\) ist \(|QM|=|MT|\) (gelb) und daraus folgt, dass die rechtwinkligen Dreiecke \(\triangle XTM\) und \(\triangle RMQ\) ebenfalls kongruent sind und somit die Strecken \(|XT|\) und \(|RM|\) (lila) gleich lang sind. Weiter ist im Dreieck \(\triangle XTM\)$$|XT| = |MT| \cdot \sin(x) = |SP|\cdot \sin(x)=\sin^2(x)$$und nun kann man direkt an der Strecke \(OT\) ablesen:$$\cos(2x) = |OC| = 1 - 2|XT| = 1-2\sin^2(x)$$