Bestimme das Längenverhältnis von Höhe und Hypotenuse.

Question

Die Fläche eines rechtwinkligen Dreiecks ist links von der Höhe auf der Hypotenuse halb so groß, wie rechts von der Höhe auf der Hypotenuse. Bestimme das Längenverhältnis von Höhe und Hypotenuse.

Answer 1

Die Teildreiecke haben die Flächen h*p/2 und h*q/2

(p,q Hypotenusenabschnitte)

Also gilt z.B. 2p=q (oder 2q=p)

Ich nehme mal das erste.

Höhensatz ergibt h^2 =p*q also h^2 = 2p^2

==>  h= p*√2. Und c=p+q = p+2p = 3p

Also Verhältnis h:c= (p*√2) : ( 3p) =  √2 : 3

Answer 2

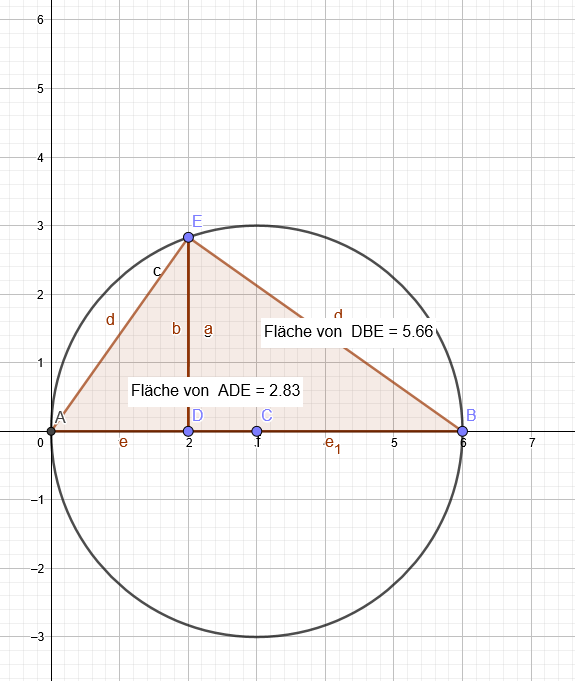
A₁ (A,H_c,C)=\( \frac{u*v}{2} \)

A₂ (,H_c,B,C)=\( \frac{(c-u)*v}{2} \)

2*A₁=A₂

2*\( \frac{u*v}{2} \)=\( \frac{(c-u)*v}{2} \)

2uv=(c-u)*v

2u=(c-u)

3u=c

u=\( \frac{c}{3} \)

\( \frac{c}{3} \)*(c-\( \frac{c}{3} \))=\( h^{2} \)

\( \frac{c}{3} \)*(\( \frac{2}{3} \)c)=\( h^{2} \)

\( h^{2} \)=\( \frac{2}{9} \)\( c^{2} \)

h=\( \frac{c}{3} \)\( \sqrt{2} \)

\( \frac{h}{c} \)=\( \frac{1}{3} \)\( \sqrt{2} \)