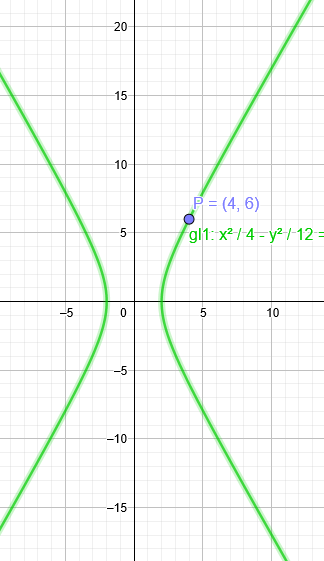
Der Punkt P ist ein beliebiger Punkt der Hyperbel. Ermittle die Gleichung der Hyperbel! P= (4|6) F1= (4|0)
\( \frac{x^2}{a^2} \)-\( \frac{y^2}{b^2} \)=1
\( b^{2} \) = \( e^{2} \)- \( a^{2} \)
e=4
\( b^{2} \) = 16- \( a^{2} \)
\( \frac{x^2}{a^2} \)-\( \frac{y^2}{16-a^2} \)=1
P= (4|6)
\( \frac{16}{a^2} \)-\( \frac{36}{16-a^2} \)=1
a=2
\( b^{2} \) = 16- 4=12
\( \frac{x^2}{4} \)-\( \frac{y^2}{12} \)=1