Hallo,
Wenn die Asymptote und \(b\) gegeben ist, kann man \(a\) leicht aus folgender Skizze bestimmen. Die Koordinate \((a,b)\) muss die Gleichung einer der Asymptoten erfüllen (siehe auch dieses Bild bei Wiki).
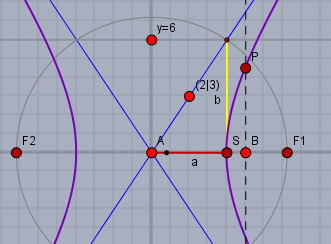
In diesem Fall die Gleichung der Gegenasymptote \(3x-2y=0\). Es gilt$$3a - 2b=0 \implies a = \frac{2b}{3}= 4$$Die gesuchte Gleichung der Hyperbel lautet somit$$\frac{x^2}{4^2}-\frac{y^2}{6^2} = 1$$und Funktion nach \(y\) nebst Ableitung ist folglich$$y = 6\sqrt{\frac{x^2}{4^2} - 1 } = \frac 32 \sqrt{x^2-4^2}\\ y' = \frac 32 \frac{x}{\sqrt{x^2-4^2}}$$An der Stelle \(x=5\) ist$$y(5)= \frac 92, \quad y'(5)= \frac 52$$Also lautet die Gleichung der Tangente \(t\) bei \(x=5\)$$t: \quad y = \frac 52(x-5) + \frac 92 = \frac 52 x - 8$$Zum Schluß die Asymptote, die Hyperbel, den Punkt \(P\) und die Tangente \(t\) zur Kontrolle in Desmos eingeben:
Gruß Werner