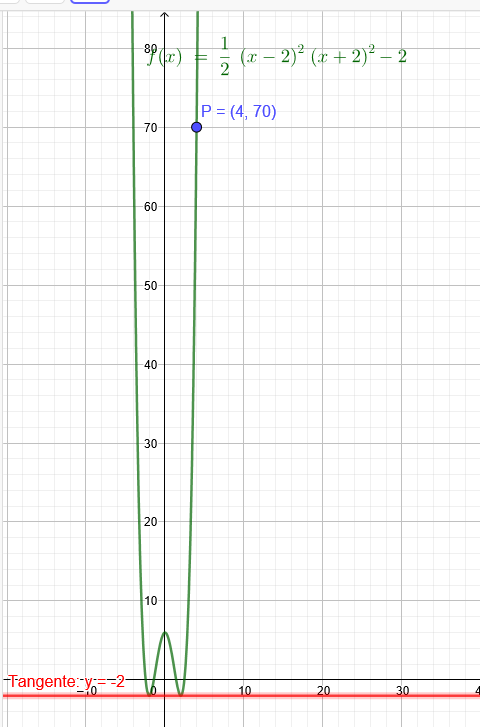
Ganzrationale Funktion vom Grad 4 gesucht

Question

Aufgabe: Gesucht ist: Ganzrationale Funktion vom Grad 4 Bedingungen: Graph ist achsensymmetrisch zur Y-Achse, Tangente im Punkt (2/-2) ist parallel zur X-Achse, Graph verläuft durch den Punkt (4/70)

Problem/Ansatz: Hallo, ich komme bei der Steckbriefaufgabe mit ganzrationaler Funktion vom Grad 4 nicht weiter.

Answer 1

Hallo und willkommen in der Mathelounge,

eine zur y-Achse symmetrische Funktion 4. Grades kann mit dieser Gleichung dargestellt werden

\(f(x)=ax^4+cx^2+e\\ f'(x)=4ax^3+2cx\)

Tangente im Punkt (2/-2) ist parallel zur X-Achse

\(f(2)=-2 \Longrightarrow 16a+4c+e=-2\\f'(2)=0\Longrightarrow 32a + 4c =0\)

Graph verläuft durch den Punkt (4/70)

\(f(4)=70\Longrightarrow 256a+16b+e=70\)

Mit diesem Gleichungssystem kannst du a, c und e bestimmen.

Gruß, Silvia

Comments

Vielen Dank, jetzt bin ich schon ein ganzes Stückchen weiter! Aber wie kann ich das Gleichungssystem lösen und und a,c,e bestimmen?

---

Du könntest z.B. das Gauß-Verfahren anwenden.

---

Aber wieso ist bei dieser Gleichung noch b enthalten? b ist doch 0?

(4)=70⟹256�+16�+�=70f(4)=70⟹256a+16b+e=70

---

Ich habe mich verschrieben. Es muss 16c heißen.

Answer 2

"Ganzrationale Funktion vom Grad 4 Bedingungen: Graph ist achsensymmetrisch zur Y-Achse, Tangente im Punkt (2|-2) ist parallel zur X-Achse, Graph verläuft durch den Punkt (4|70)"

Ich verschiebe den Graph um 2 Einheiten nach oben:

Tangente im Punkt (2|0)

doppelte Nullstellen in P(2|0) und Q(-2|0) sind Extremwerte. Weiter mit Nullstellenform der Parabel 4. Grades:

f(x)=a•(x-2)^2*(x+2)^2

P´(4|72)

f(4)=a•(4-2)^2*(4+2)^2=144a

144a=72

a=\( \frac{1}{2} \)

f(x)=\( \frac{1}{2} \)•(x-2)^2*(x+2)^2

Nun 2 Einheiten nach unten:

f(x)=\( \frac{1}{2} \)•(x-2)^2*(x+2)^2-2

Answer 3

Ansatz: f(x)=ax⁴+bx²+c wegen Achsensymmetrie.

f '(x)=4ax³+2bx

f(2)=-2  führt zu -2=16a+4b+c

f '(2)=0 führt zu 0=32a+4b

f(4)=70 führt zu 70=256a+16b+c

Löse das System und setze a, b und c in den Ansatz ein.

Answer 4

f(x) = ax^4+bx^2+c

f '(x) = 4ax^3+2bx

f(2)= -2

f '(2) = 0

f(4) = 70

16a+4b+c= -2

32a +4b = 0

256a+16b+c= 70

Comments

4⁴=256     .....