Berechne die Ableitung von Funktion f an der Stelle x0

Question

Aufgabe:

Berechne die Ableitung von Funktion f

Text erkannt:

\( f(x)=\frac{x^{2}-10 x+25}{x^{2}+4 x+3} \)

an der Stelle x0 = 1

Problem/Ansatz:

Hi, ich hab versucht die Aufgabe mit der h-Methode zu lösen komme aber irgendwie nicht mehr weiter. Kann mir jemand den Lösungsweg bitte zeigen?

Answer 1

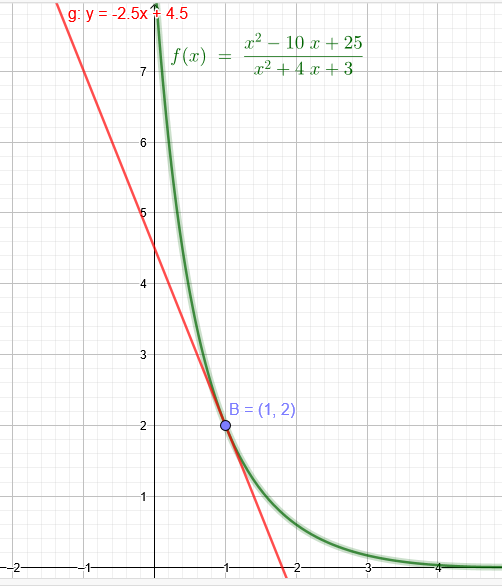
\(f(x)=\frac{x^{2}-10 x+25}{x^{2}+4 x+3} \)    x₀=1

Ableitung mittels der Quotientenregel:

\( \frac{d f(x)}{d x}=f^{\prime}(x)=\frac{(2 x-10) \cdot\left(x^{2}+4 x+3\right)-\left(x^{2}-10 x+25\right) \cdot(2 x+4)}{\left(x^{2}+4 x+3\right)^{2}} \)

\( f^{\prime}(1)=\frac{(2 \cdot 1-10) \cdot\left(1^{2}+4 \cdot 1+3\right)-\left(1^{2}-10 \cdot 1+25\right) \cdot(2 \cdot 1+4)}{\left(1^{2}+4 \cdot 1+3\right)^{2}}=-2,5 \)