Beweisen, dass A und B gleich lang sein sollen

Question

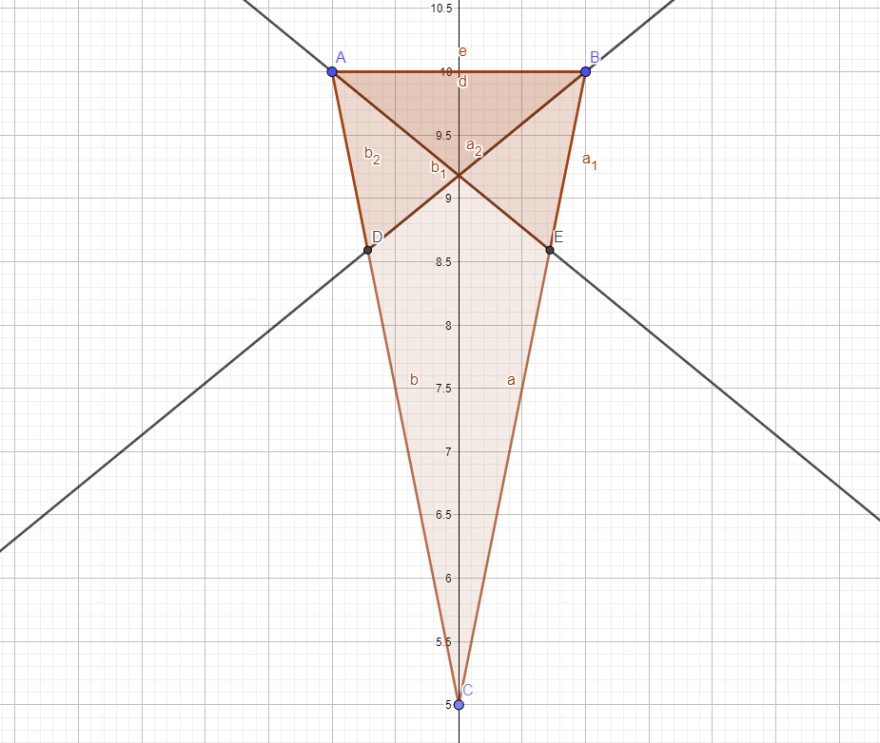
Spitzwinklige Dreieck mit gleich langen höhen von A und B

Hallo zusammen ich bräuchte Hilfe bei der Aufgabe:

Beweisen Sie: Wenn ein spitzwinkliges Dreieck Δ ABC gleichschenklig mit |ACI = |BC| ist, dann sind die von A und B ausgehenden Höhen gleich lang.

Ich benötige die Kongruenzsätze um dies zu beweisen.

Als Voraussetzung kann ich notieren, dass AC = BC <=> A = B.

Wenn ich die höhe im Punkt A und B eintrage, erhalte ich jeweils einen Schnittpunkt auf b und a, das wären D und E. Nun weiß ich aber leider nicht wie ich weiter bzw. starten soll um festzustellen, das die Höhe von A ( AE ) und die Höhe von B ( BD ) gleich lang sind.

Vielen Dank für die Hilfe :)

Comments

gleichschenklig mit |I = || ist, dann sind die von und ausgehenden Höhen gleich lang.

Was möchtest Du damit mitteilen?

Und wie ist der Titel zu verstehen? A und B sind Punkte, die können nicht gleich lang sein.

---

Entschuldige, ist mir wohl entgangen, hab ich überarbeitet

---

Entschuldige, ist mir wohl entgangen, hab ich überarbeitet

Mitnichten. Im Titel steht immer noch etwas von zwei gleich langen Punkten.

---

Leider kann ich es nicht mehr bearbeiten, da ich die Aufgabenstellung überarbeitet habe und ich dachte das es durch die Aufgabenstellung klar wird. Es soll sein " Beweisen, dass die ausgehenden Höhen von A und B gleich lang sind".

Answer 1

Hallo

in deiner Zeichnung sind das keine Höhen, sie stehen nicht senkrecht!

bei richtiger Zeichnung sind dei 2 Dreiecke ADB und BEA kongruent.  Sehe AB, rechter Winkel und  die Winkel bei A bzw B sind gleich, weil die Winkel bei A und B auch gleich sind.

einfacher; die Fläche s1*h1/2 =A=s2*h2 und s1=s2

Gruß lul