Zeigen Sie: Die Strecken CD und CE und sind genau dann gleich lang, wenn sich die Geraden AE und BD rechtwinklig …

Question

Aufgabe:

Gegeben ist ein gleichschenklig-rechtwinkliges Dreieck ABC mit dem rechten Winkel bei C. Die Punkte D und E liegen außerhalb des Dreiecks auf den Halbgeraden AC bzw. CB. Zeigen Sie: Die Strecken CD und CE und sind genau dann gleich lang, wenn sich die Geraden AE und BD rechtwinklig schneiden.

Comments

Hier eine Skizze zu der Aufgabe:

Answer 1

Zwei gleichschenklig-rechtwinklige Dreiecke (rot und grün) haben die abgebildete Lage zueinander:

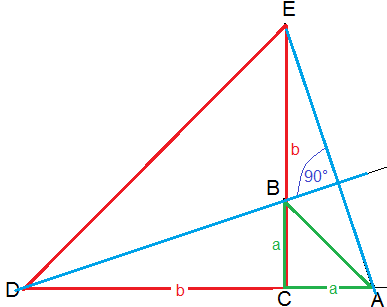
Dann hat die Gerade DB die Steigung \( \frac{a}{b} \) und die Gerade AE die Steigung \( \frac{b}{-a} \). Steigungen sind genau dann negativ reziprok zueinander, wenn sie senkrecht zueinander sind.