Halllo Roland,
eigentlich ganz einfach, wenn man es sieht ;-)
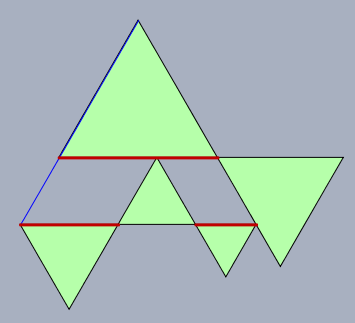
Benennt man die Seiten der fünf Dreiecke mit aufsteigender Größe mit \(s_0\) bis \(s_4\), so sieht man durch Vergleich der roten Streckenstücke, dass $$s_4=s_2+s_0$$Da die \(s_i\) eine geometrische Folge mit der Basis \(q\) bilden sollen, ist$$q^4 = q^2 + 1 \implies q^2 = \phi \quad \text{wg.}\space q,q^2 \gt 1$$Also ist das gesuchte Verhältnis \(q=\sqrt{\phi}\).
Gruß Werner