Bestimmen Sie die Kurvenintegrale von f entlang der folgenden Wege:

Question

Aufgabe:

Sei f : ℂ \ { 1 - i, -1 + i } ↦ ℂ holomorph mit

\( \int \limits_{\gamma_{1}} f(z) \mathrm{d} z=1, \quad \int \limits_{\gamma_{2}} f(z) \mathrm{d} z=\mathrm{i}, \quad \int \limits_{\gamma_{3}} f(z) \mathrm{d} z=\pi \),

wobei die Wege {\gamma_{1}}, {\gamma_{2}} und {\gamma_{3}} durch

gegeben sind. Bestimmen Sie die Kurvenintegrale von f entlang der folgenden Wege:

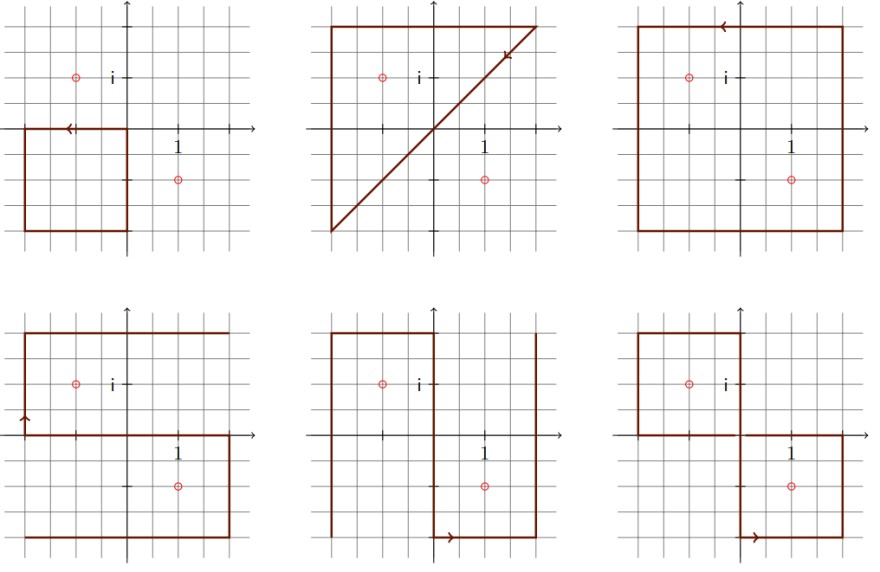
Text erkannt:

\( \square \)

Problem/Ansatz:

Ich habe bei der Aufgabe damit angefangen die einzelnen Wege zu parametrisieren. Mir ist aber nicht so richtig klar, wie ich die Kurvenintegrale bestimmen soll. Es wäre sehr hilfreich, wenn mir jemand einen Hinweis geben könnte, wie ich mit dieser Aufgabe anfangen könnte. :)

Vielen lieben Dank!

Answer 1

Hallo

du sollst die neuen Weg durch Zusammensetzung der gegebenen Wege bestimmen, deren Wegintegrale du kennst, achte dabei auf die angegebenen Richtungen, dreht sich die um wird das Integral das negative.

Gruß lul

Comments

Brauche ich dafür die Parametrisierung der obigen 3 Abbildungen?

---

Ich verstehe auch nicht so ganz, in wie weit mir die Wege gegeben sind. Ich habe ja nur bspw. bei Gamma 1 das Integral von f(z) dz aber keine Funktion gegeben. Nur das Ergebnis =1. Wie kann ich das verwenden?

---

Hey, ich hänge an dergleichen Aufgabe, für die Wege 2 und 3 ist das ja relativ leicht. Kann mir jemand vielleicht einen Tipp für weg 1 geben? Ich hab es mit einer Parametrisierung der obigen Wege versucht, komme aber zu keinen guten Ergebnis.

---

Hallo

wie hast du denn 2 und 3 parametrisiert? 1 ist doch am Anfang fast wie 3?

lul

---

Ergänzung meiner Antwort:

due kannst die gegebenen Wege zu 2 geschlossenen Ergänzen, damit kennst du das Residuum in den Punkten -1+i und  1-i

damit  sindalle Wegeintegrale, die um einen der Punkte (oder 2 Führen)  durch den Residuensatz bekannt, die nicht geschlossenen Wege- wie etwa 4 und 5- durch γ2 schließen.

Gruß lul