Lineare Gleichungssysteme | komische Notation

Question

Ich soll zeigen, dass das lineare Gleichungssystem:

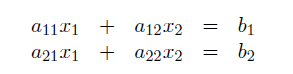
Text erkannt:

\( a_{11} x_{1}+a_{12} x_{2}=b_{1} \)
\( a_{21} x_{1}+a_{22} x_{2}=b_{2} \)

mit a_ij , b_i ∈ ℝ genau dann eindeutig lösbar ist, wenn a₁₁ a₂₂ - a₁₂ a₂₁ ≠ 0. In diesem Fall soll ich nun die Lösung des Gleichungssystems angeben.

Ich bin sehr verwirrt wegen der Notation hier..

Answer 1

Schau mal dort:

https://www.mathelounge.de/892000/gleichungssystem-analyse-hilfe

Comments

ich hab das bis zum schritt wo man x2 ausklammert verstanden, danach komme ich nicht weiter, womit soll ich denn da dividieren?

---

Durch die ganze Klammer dividieren, das ist auch

(bis auf das VZ) der Term, der nicht 0 sein darf.

---

der Term der 0 ist, ist doch gar nicht mehr da oder nicht?

---

x2( a12a21 -a22a11) = b1a21- b2a11  | und jetzt / (a12a21 - a22a11)

oder wie?

---

Ja genau so !