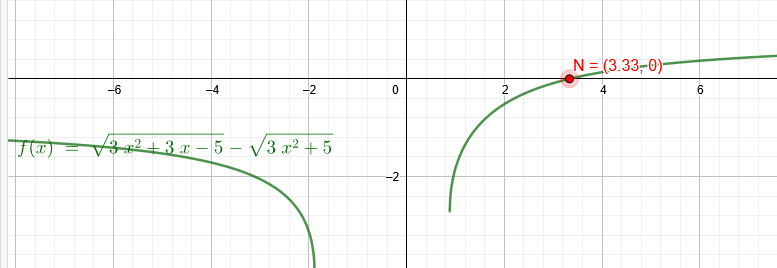Zwei Wurzelgleichungen subtrahieren

Question

Aufgabe:

Guten Tag,

ich wollte wissen, wie ich diese Wurzelgleichung lösen kann.

f(x)=sqrt(3*x^2+3*x-5)-sqrt(3*x^2+5)

Problem/Ansatz:

Was ich bisher versucht habe, war's beide Seiten zu quadrieren, um das Wurzelzeichen zu lösen. Wenn ich es hierauf vereinfache, bleibt nur noch das 3x übrig.

Answer 1

f(x)=\( \sqrt{(3*x^2+3*x-5)} \) -\( \sqrt{(3*x^2+5)} \) 

Vielleicht ist die Nullstelle gesucht:

\( \sqrt{(3*x^2+3*x-5)} \) -\( \sqrt{(3*x^2+5)} \)=0

\( \sqrt{(3*x^2+3*x-5)} \)=\( \sqrt{(3*x^2+5)} \) |\( ^{2} \)

3*x^2+3*x-5=3*x^2+5|-3x^2

3*x=10

x=\( \frac{10}{3} \)

Comments

Vielen Dank, ich finde es mit der grafischen Darstellung noch interessanter!