Aufgabe:
Da ich vergessen habe die Bilder hochzuladen, stelle ich die Frage erneut:
Text erkannt:
\( =\frac{\mathrm{p}_{1} V_{1}^{\gamma}}{-\gamma+1} \cdot\left(V_{1}^{-\gamma+1}-V_{2}^{-\gamma+1}\right) \)
\( V_{1}^{-\gamma+1}\left(1-\frac{V_{2}^{-\gamma+1}}{V_{1}^{-\gamma+1}}\right) \)
\( =\frac{\mathrm{p}_{1} V_{1}^{\gamma} \cdot V_{1}^{-\gamma+1}}{-\gamma+1} \cdot\left(1-\frac{V_{2}^{-\gamma+1}}{V_{1}^{-\gamma+1}}\right)=\frac{\mathrm{p}_{1} V_{1}}{\gamma-1} \cdot\left(\frac{V_{1}^{\gamma-1}}{V_{2}^{\gamma-1}}-1\right) \quad \) Adiabatische Volumenarbeit
(V \( =V_{A}, V_{2}=V_{E} \) )
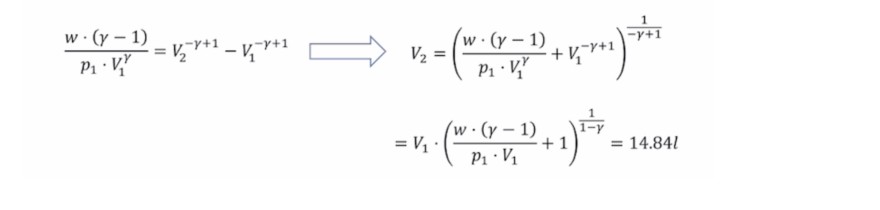
Text erkannt:
\( \begin{aligned} \frac{w \cdot(\gamma-1)}{p_{1} \cdot V_{1}^{\gamma}}=V_{2}^{-\gamma+1}-V_{1}^{-\gamma+1} & \Rightarrow V_{2}=\left(\frac{w \cdot(\gamma-1)}{p_{1} \cdot V_{1}^{\gamma}}+V_{1}^{-\gamma+1}\right)^{\frac{1}{-\gamma+1}} \\ &=V_{1} \cdot\left(\frac{w \cdot(\gamma-1)}{p_{1} \cdot V_{1}}+1\right)^{\frac{1}{1-\gamma}}=14.84 l \end{aligned} \)
Ich kann hier den letzten Schritt nachvollziehen. Wieso wurde aus V2^-y+1 / V2^-y+1 → V1^y-1/ V2^Y-1??
Also warum dreht sich der Bruch und warum ändert sich das Vorzeichen bei -y+1? Warum wird aus -y+1 ein +y-1?
Hat man hier den Kehrwert gebildet?
Wenn ja, wie? Gibt´s hier eine bestimmte Regel, die ich anwenden muss? Könnt ihr mir weiterhelfen?
Gleiches gilt auch für das 2. Beispiel. Hier kann ich den letzen Schritt auch nicht nachvollziehen.
Über eine Rückmeldung würde ich mich wirklich sehr freuen!