Bestimmen Sie das neutrale Element in G.

Question

Aufgabe:

Sei \( G=\{a, b, c\} \) eine Menge, von der wir wissen, dass sie zusammen mit einer Verknüpfung · eine Gruppe ist. Des Weiteren sei bekannt, dass in \( G \) die Gleichheit \( a b=a \) gilt.
(i) Bestimmen Sie das neutrale Element in \( G \).
(ii) Vervollständigen Sie die Verknüpfungstafel für \( G \)

                                                

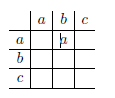
(iii) Finden Sie eine Untergruppe \( G^{\prime} \subset S_{3} \) und einen injektiven Homomorphismus \( f: G \rightarrow S_{3} \), so dass \( f(G)=G^{\prime} \) gilt. Hinweis: Es genügt, ein passendes Element \( f(a) \in S_{3} \) zu finden.

Problem/Ansatz:

Sei \( G=\{a, b, c\} \) eine Menge, von der wir wissen, dass sie zusammen mit einer Verknüpfung · eine Gruppe ist. Des Weiteren sei bekannt, dass in \( G \) die Gleichheit \( a b=a \) gilt.
(i) Bestimmen Sie das neutrale Element in \( G \).
(ii) Vervollständigen Sie die Verknüpfungstafel für \( G \)

                                                                                            

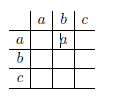
(iii) Finden Sie eine Untergruppe \( G^{\prime} \subset S_{3} \) und einen injektiven Homomorphismus \( f: G \rightarrow S_{3} \), so dass \( f(G)=G^{\prime} \) gilt. Hinweis: Es genügt, ein passendes Element \( f(a) \in S_{3} \) zu finden.

Answer 1

(i): Sei \(e\) das neutrale Element, dann gilt \(ab=a=ae\). Multiplikation

mit \(a^{-1}\) von links liefert \(b=e\), also ist \(b\) das neutrale Element.

(ii): Nun sieht die Tabelle also so aus

	a	b	c
a		a
b	a	b	c
c		c

In einer Gruppentafel kommt jedes Element in jeder Zeile und
jeder Spalte genau einmal vor.
Also kann \(a\circ c\) nicht gleich \(c\) sein, sondern muss
zwangsläufig \(b\) sein. Dann ist aber \(a\circ a=c\)Damit liegt
auch die untere Zeile eindeutig fest:

	a	b	c
a	c	a	b
b	a	b	c
c	b	c	a

Die Gruppe ist \(\{b=a^0,a,a^2=c\}\), also zyklisch von \(a\) erzeugt.
(iii): Damit bietet sich an, die Elemente von \(G\) auf die Elemente einer
dreielementigen Untergruppe \(G'\) von \(S_3\) abzubilden:
\(f(a)=(1\; 2\; 3),\; f(c)=(1\; 3\; 2),\; f(b)=id\).