Hallo zusammen
könnte mir jemand bei folgender Kombinatorik-Aufgabe helfen?
Ein Zufallsgenerator erzeugt mit Ziffern aus {0, 1, ... ,9} Ziffernblöcke der Länge 4. Geben Sie mit Begründung die Wahrscheinlichkeiten für folgende fünf Ereignisse an.
a) Alle Ziffern sind verschieden.
b) Genau ein Paar gleiche Ziffern
c) Genau zwei Paare gleicher Ziffern
d) Genau drei gleiche Ziffern
e) vier gleiche Ziffern
Viel hab ich davon leider noch nicht geschafft. Zur Orientierung habe ich mir folgende Abbildung genommen.
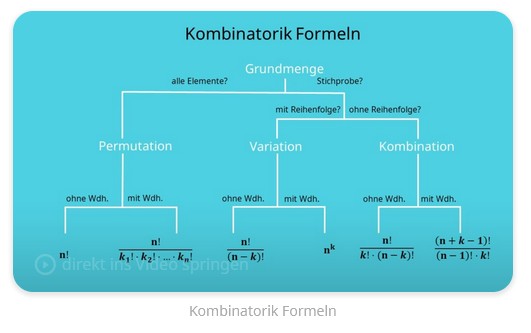
Quelle: https://studyflix.de/statistik/kombinatorik-1076
Zu a)
Erstmal muss man ja wissen, wie viele verschiedene Ziffernblöcke es insgesamt geben könnte ??
Also eine Stichprobe, mit Reihenfolge (damit kein Block doppelt vorkommt?) und mit Wiederholung, da die Zufallszahlen auch in mehreren Blöcken vorkommen können.
Also n^k = 10^4 unterschiedliche Kombinationsmöglichkeiten der Ziffern in den 4er Blöcken.
Dann habe ich gedacht, muss man herausfinden, wie viele Ziffernblöcke nur unterschiedliche Zahlen enthalten.
Also eine Stichprobe, mit Reihenfolge (damit wieder nix doppelt ist) und ophne Wiederholung (weil unterschiedliche zahlen). 10!/(10-4)! = 5040.
Und dann zum Schluss die Wahrscheinlichkeit dafür (nach Laplace) = Anzahl günstiger Fälle / Anzahl aller möglichen Fälle = 5040/10000 = 0,504
Ist mein Gedankengang da richtig? Für die anderen habe ich leider noch keine Lösung.