Aufgabe:
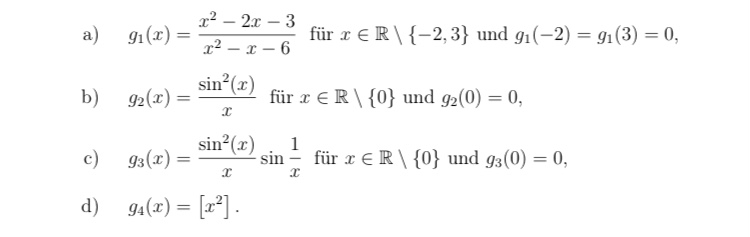
Text erkannt:
a) \( g_{1}(x)=\frac{x^{2}-2 x-3}{x^{2}-x-6} \) für \( x \in \mathbb{R} \backslash\{-2,3\} \) und \( g_{1}(-2)=g_{1}(3)=0 \),
b) \( g_{2}(x)=\frac{\sin ^{2}(x)}{x} \) für \( x \in \mathbb{R} \backslash\{0\} \) und \( g_{2}(0)=0 \),
c) \( g_{3}(x)=\frac{\sin ^{2}(x)}{x} \sin \frac{1}{x} \) für \( x \in \mathbb{R} \backslash\{0\} \) und \( g_{3}(0)=0 \),
d) \( g_{4}(x)=\left[x^{2}\right] \).
Problem/Ansatz:
Bestimmen Sie die Unstetigkeitsstellen und die Art der gefun-
denen Unstetigkeit für die Funktionen gk: R→Rmit k = 1,2,3,4. Begründen Sie Ihre
Antwort durch Betrachtung der entsprechenden Grenzwerte.